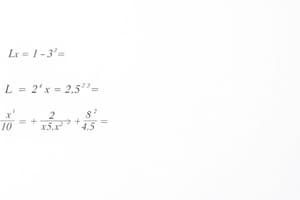Podcast
Questions and Answers
What characterizes a vertical asymptote in a rational function?
What characterizes a vertical asymptote in a rational function?
- It only exists when the degree of the numerator is higher.
- It is represented by the zeros of the denominator. (correct)
- It is always a line that the curve touches.
- It is a horizontal line that the curve approaches.
How is the horizontal asymptote determined for rational functions?
How is the horizontal asymptote determined for rational functions?
- By the leading coefficient of the numerator alone.
- By comparing the degrees of the numerator and the denominator. (correct)
- By the zeroes of the numerator.
- It is determined by the coefficients of all the terms.
When does an oblique asymptote exist in a rational function?
When does an oblique asymptote exist in a rational function?
- Oblique asymptotes never exist for rational functions.
- When the degree of the numerator is larger than the degree of the denominator. (correct)
- Only when both degrees are equal.
- When the degree of the numerator is less than the denominator.
What condition indicates that there is no horizontal asymptote in a rational function?
What condition indicates that there is no horizontal asymptote in a rational function?
What is the nature of a curve concerning asymptotes?
What is the nature of a curve concerning asymptotes?
What is a table of values for rational functions used to represent?
What is a table of values for rational functions used to represent?
Which best describes a vertical asymptote?
Which best describes a vertical asymptote?
How are vertical asymptotes determined in rational functions?
How are vertical asymptotes determined in rational functions?
What does the term 'asymptote' refer to in mathematical terms?
What does the term 'asymptote' refer to in mathematical terms?
Which method can be used to graph a rational function accurately?
Which method can be used to graph a rational function accurately?
Which statement about asymptotes is incorrect?
Which statement about asymptotes is incorrect?
What is the primary purpose of analyzing asymptotes in rational functions?
What is the primary purpose of analyzing asymptotes in rational functions?
What is an essential step in constructing a table of values for rational functions?
What is an essential step in constructing a table of values for rational functions?
What characterizes a horizontal asymptote in a rational function?
What characterizes a horizontal asymptote in a rational function?
When the degree of the numerator is greater than the degree of the denominator, what is the result concerning horizontal asymptotes?
When the degree of the numerator is greater than the degree of the denominator, what is the result concerning horizontal asymptotes?
If the degree of both the numerator and denominator of a rational function are equal, what determines the horizontal asymptote?
If the degree of both the numerator and denominator of a rational function are equal, what determines the horizontal asymptote?
What is true about oblique asymptotes in rational functions?
What is true about oblique asymptotes in rational functions?
How is the horizontal asymptote expressed when the degree of the numerator is less than that of the denominator?
How is the horizontal asymptote expressed when the degree of the numerator is less than that of the denominator?
In the context of horizontal asymptotes, what does the term 'leading coefficient' refer to?
In the context of horizontal asymptotes, what does the term 'leading coefficient' refer to?
Which behavior indicates that a rational function approaches its horizontal asymptote?
Which behavior indicates that a rational function approaches its horizontal asymptote?
Which statement accurately reflects what happens when analyzing horizontal asymptotes of rational functions?
Which statement accurately reflects what happens when analyzing horizontal asymptotes of rational functions?
Why is it important to select values close to where the function is undefined?
Why is it important to select values close to where the function is undefined?
How do you determine the vertical asymptote of a rational function?
How do you determine the vertical asymptote of a rational function?
What is the role of constructing a table of values when analyzing a rational function?
What is the role of constructing a table of values when analyzing a rational function?
What information about the degrees of the numerator and denominator helps in finding the horizontal asymptote?
What information about the degrees of the numerator and denominator helps in finding the horizontal asymptote?
When evaluating the function at integers less than and greater than 1, what is primarily observed?
When evaluating the function at integers less than and greater than 1, what is primarily observed?
What is a property of the points where the function intersects the vertical asymptote?
What is a property of the points where the function intersects the vertical asymptote?
What is the effect of selecting a wide range of values when constructing a table for a rational function?
What is the effect of selecting a wide range of values when constructing a table for a rational function?
If a rational function has a degree of the numerator greater than the degree of the denominator, what generally happens?
If a rational function has a degree of the numerator greater than the degree of the denominator, what generally happens?
Flashcards are hidden until you start studying
Study Notes
Objectives of the Lesson
- Construct tables of values for rational functions correctly.
- Determine the asymptotes of rational functions accurately.
- Graph rational functions with precision.
Key Concepts
- Table of Values: A collection of values that satisfy a given rational function, helpful for understanding the function's behavior at specific points.
- Asymptote: A line that a curve approaches but never intersects.
Types of Asymptotes
- Vertical Asymptote:
- A vertical line where the function is undefined, determined by the zeroes of the denominator.
- Horizontal Asymptote:
- A horizontal line indicating the behavior of the function as it approaches infinity. Determined by comparing the degrees of the numerator and denominator:
- If the degree of the numerator is less than the denominator, the horizontal asymptote is the line (y=0).
- If they are equal, the horizontal asymptote is (y=\frac{a}{b}) where (a) and (b) are leading coefficients of the numerator and denominator respectively.
- If the degree of the numerator is greater, there is no horizontal asymptote.
- A horizontal line indicating the behavior of the function as it approaches infinity. Determined by comparing the degrees of the numerator and denominator:
- Oblique Asymptote:
- A line that the graph approaches when the degree of the numerator is one higher than the degree of the denominator. Found via polynomial long division.
Constructing a Table of Values
- Choose values for the independent variable to substitute into the function.
- Pay attention to points where the function becomes undefined (typically where the denominator is zero).
- Select values around these points to illustrate function behavior.
Graphing Rational Functions
- Use the constructed table of values to plot points on a graph.
- Identify and draw the asymptotes as guiding lines, recognizing that the graph will approach but never cross vertical and horizontal asymptotes.
Practice Activities
- Individual practice includes constructing a table of values for a given rational function and determining its vertical and horizontal asymptotes.
- Group practice involves sketching the graph of a specified rational function, reinforcing understanding of its behavior and asymptotic behavior.
Synthesis Questions
- Explore the different methods to represent rational functions and the importance of doing so.
- Discuss whether a corresponding value of (y) exists for any given (x) in a rational function.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.