Podcast
Questions and Answers
Construire le point M tel que $\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{AC}$
Construire le point M tel que $\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{AC}$
Le point M est le sommet opposé au point A du parallélogramme ABMC.
Construire le point N tel que $\overrightarrow{BN} = \overrightarrow{CA} + \overrightarrow{CB} + \overrightarrow{BC}$
Construire le point N tel que $\overrightarrow{BN} = \overrightarrow{CA} + \overrightarrow{CB} + \overrightarrow{BC}$
Le point N est tel que $\overrightarrow{BN} = \overrightarrow{CA} + 2\overrightarrow{BC}$. Par conséquent, le point N est le symétrique du point A par rapport au point C.
Construire le point P tel que $\overrightarrow{PA} = \overrightarrow{AC} + \overrightarrow{BC} + \overrightarrow{AB}$
Construire le point P tel que $\overrightarrow{PA} = \overrightarrow{AC} + \overrightarrow{BC} + \overrightarrow{AB}$
Le point P est tel que $\overrightarrow{PA} = \overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{BC}$. P correspond au barycentre du système {(A,1),(B,1),(C,1)}. Ce barycentre est donc le centre de gravité du triangle.
Déterminer le domaine de définition de $f(x)$
Déterminer le domaine de définition de $f(x)$
Déterminer $f(2)$ et $f(-2)$
Déterminer $f(2)$ et $f(-2)$
Démontrer que $f(x)$ admet un point d'inflexion en 0.
Démontrer que $f(x)$ admet un point d'inflexion en 0.
Résoudre l'équation $f(x)=cos(x)$
Résoudre l'équation $f(x)=cos(x)$
Établir le tableau de variation de $f$.
Établir le tableau de variation de $f$.
Étudier le signe de $f$.
Étudier le signe de $f$.
Donner le minimum de $f$ sur $[-1,7]$
Donner le minimum de $f$ sur $[-1,7]$
Flashcards
Construire un point (point M)
Construire un point (point M)
Placer un point M de manière à ce que la distance AM soit égale à la somme des distances AB et AC.
Construire un point (point N)
Construire un point (point N)
Placer un point N de manière à ce que la distance BN soit égale à la somme des distances BC, CA et CB.
Construire un point (point P)
Construire un point (point P)
Placer un point P de manière à ce que la distance PA soit égale à la somme des distances AC, BC et AB.
Domaine de définition d'une fonction (f)
Domaine de définition d'une fonction (f)
Signup and view all the flashcards
Cosinus
Cosinus
Signup and view all the flashcards
Study Notes
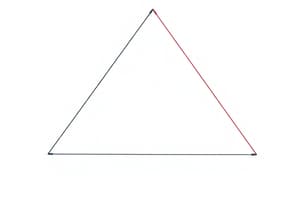
Triangle ABC
- A triangle named ABC is given.
- Points M, N, and P are constructed to satisfy certain conditions relating to the sides of the triangle.
Function f(x)
- The function f(x) is defined on the interval [-5, 2].
- Calculate f(2) and f(-2).
- Find the values which the function maps to -1 from input.
- Solve where the function is less than -1.
- Establish the variation/trend table for the function f(x).
- Create the sign table for the function f(x).
- Determine the minimum value of the function f(x)
- Solve for f(x) = 2
- Find the minimum value of the function in the interval [-2, 4].
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.