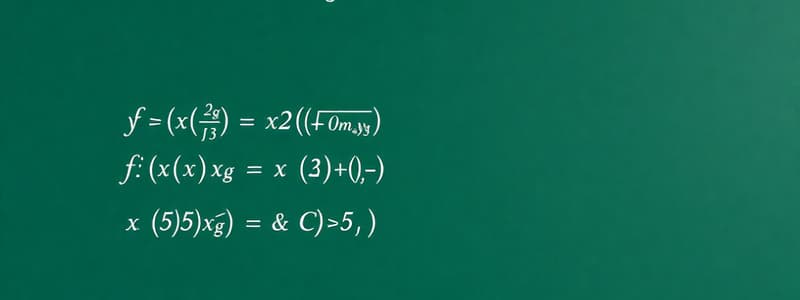Podcast
Questions and Answers
What is the value of g(x) when x is not equal to 5?
What is the value of g(x) when x is not equal to 5?
- 0
- x + 5 (correct)
- 5
- 10
At which point does the function g(x) have a point of discontinuity?
At which point does the function g(x) have a point of discontinuity?
- x = 0
- x = -5
- x = 5 (correct)
- x = 1
What is the value of the limit of g(x) as x approaches 5?
What is the value of the limit of g(x) as x approaches 5?
- 0
- Undefined
- 10 (correct)
- 5
For x ≠ 5, how can g(x) be simplified?
For x ≠ 5, how can g(x) be simplified?
What type of discontinuity does g(x) have at x = 5?
What type of discontinuity does g(x) have at x = 5?
How is the discontinuity in g(x) removed?
How is the discontinuity in g(x) removed?
What is the redefined value of g(5) that makes g(x) continuous?
What is the redefined value of g(5) that makes g(x) continuous?
What is the original form of g(x) for x ≠ 5?
What is the original form of g(x) for x ≠ 5?
What does it mean for g(x) to have a 'hole' at x = 5?
What does it mean for g(x) to have a 'hole' at x = 5?
After removing the discontinuity, what is true about g(x)?
After removing the discontinuity, what is true about g(x)?
When x = 1, what is g(x) equal to?
When x = 1, what is g(x) equal to?
How can you determine that $g(x)$ has a removable discontinuity at $x=5$?
How can you determine that $g(x)$ has a removable discontinuity at $x=5$?
In the original definition of $g(x)$, what value is assigned to $g(5)$?
In the original definition of $g(x)$, what value is assigned to $g(5)$?
What algebraic technique is used to simplify the expression $\frac{x^2 - 25}{x - 5}$?
What algebraic technique is used to simplify the expression $\frac{x^2 - 25}{x - 5}$?
For what values of $x$, other than $x=5$, is the simplified form $g(x)=x+5$ valid?
For what values of $x$, other than $x=5$, is the simplified form $g(x)=x+5$ valid?
What is the value of $g(x)$ when $x=0$?
What is the value of $g(x)$ when $x=0$?
What is the significance of the limit existing as $x$ approaches $5$ for the given function?
What is the significance of the limit existing as $x$ approaches $5$ for the given function?
If $g(x)$ were not redefined at $x=5$, what would be the nature of the function at that point?
If $g(x)$ were not redefined at $x=5$, what would be the nature of the function at that point?
What characteristic of the original function $\frac{x^2 - 25}{x - 5}$ leads to the discontinuity at $x=5$?
What characteristic of the original function $\frac{x^2 - 25}{x - 5}$ leads to the discontinuity at $x=5$?
What is the primary reason for making $g(x)$ continuous everywhere?
What is the primary reason for making $g(x)$ continuous everywhere?
Flashcards
Point of Discontinuity
Point of Discontinuity
A function that is not continuous at a specific point.
Removable Discontinuity
Removable Discontinuity
Since the limit exists and matches the redefined value g(5) = 10, the discontinuity is removable.
Limit Value at x=5
Limit Value at x=5
The limit of g(x) as x approaches 5 is 10. lim (x->5) g(x) = 10
Simplified g(x)
Simplified g(x)
Signup and view all the flashcards
Continuity Definition
Continuity Definition
Signup and view all the flashcards
Study Notes
- Smart Stella Chidinma, CSC/23/6891 is the author of the notes.
Function definition
- g(x) = (x²-25)/(x-5) when x ≠ 5
- g(x) = 10 when x = 5
Analysis of g(x)
- Considering the function g(x)
- When x = 1, initially g(x) = (x²-25)/(x-5) is evaluated as (5²-25)/(5-5) = 0/0.
- The function has a point of discontinuity at x = 5.
Simplification for x ≠ 5
- For x ≠ 5, g(x) = (x²-25)/(x-5) = ((x-5)(x+5))/(x-5) = x + 5.
Limit Evaluation
- Finding the limit as x approaches 5.
- For x ≠ 5, g(x) = x + 5.
- The limit of g(x) as x approaches 5 is lim (x→5) g(x) = 5 + 5 = 10.
Discontinuity
- g(x) has a hole at x = 5 due to the (x²-25)/(x-5) form.
- The discontinuity is removable because the limit exists and matches the redefined value g(5) = 10.
- The discontinuity is removed by explicitly defining g(5) = 10, making g(x) continuous everywhere.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.