Z = px + qy + p^2 + q^2
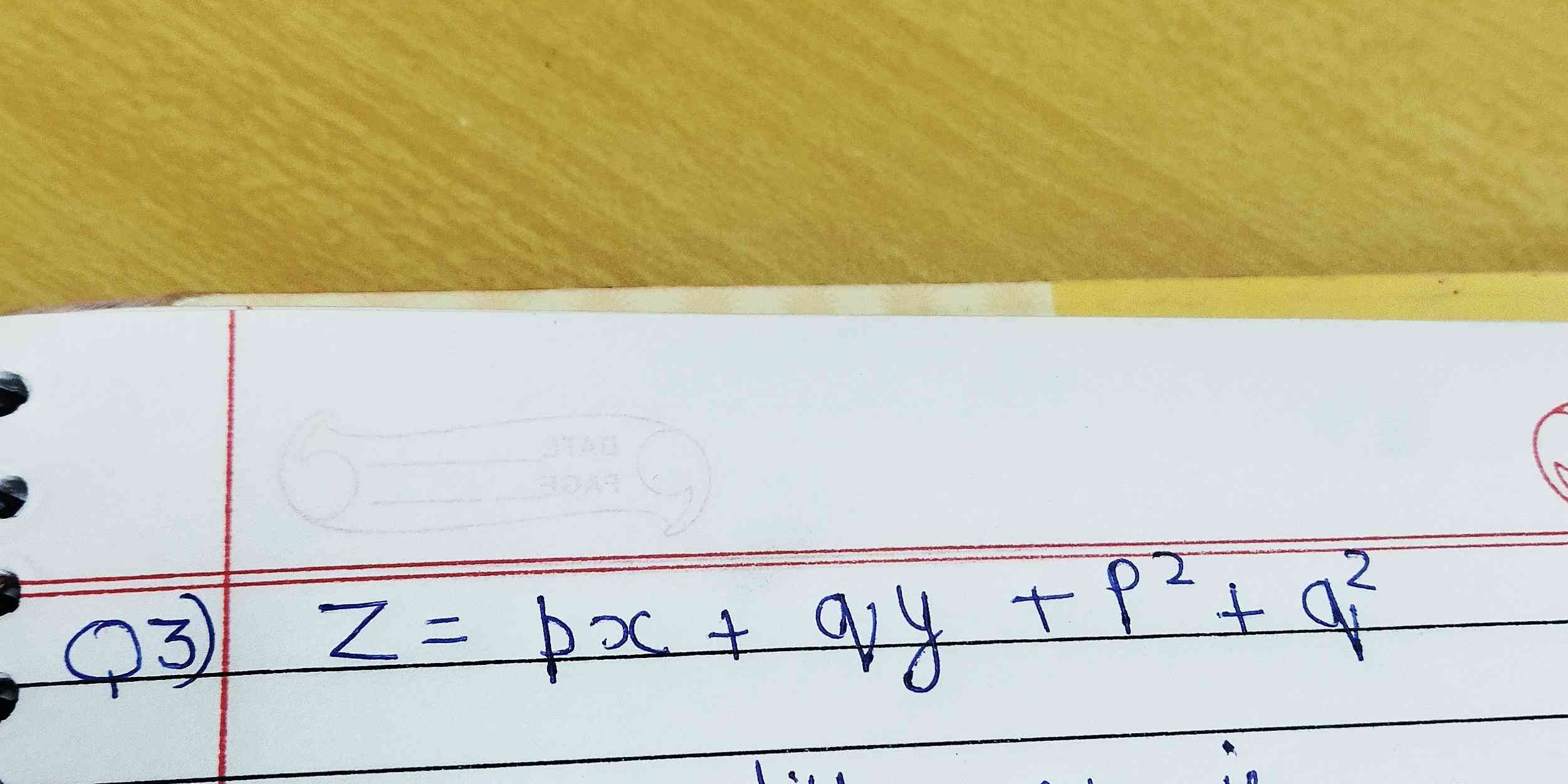
Understand the Problem
The question presents an equation Z = px + qy + p^2 + q^2. It appears to be the start of a problem, likely involving partial differential equations or related concepts. The goal is likely to solve or analyze this equation. A common approach might involve using techniques like the Charpit's method or other suitable methods based on the context of the course.
Answer
$Z = ax + by + a^2 + b^2$
Answer for screen readers
$Z = ax + by + a^2 + b^2$
Steps to Solve
- Identify the type of equation
The given equation $Z = px + qy + p^2 + q^2$ is a non-linear first-order partial differential equation. Here, $p = \frac{\partial Z}{\partial x}$ and $q = \frac{\partial Z}{\partial y}$.
- Apply Charpit's method
Charpit's method is used to solve non-linear first-order PDEs of the form $f(x,y,z,p,q) = 0$. In this case, $f(x,y,z,p,q) = px + qy + p^2 + q^2 - Z = 0$.
- Write down Charpit's equations
Charpit's equations are given by:
$$ \frac{dp}{f_x + p f_z} = \frac{dq}{f_y + q f_z} = \frac{dz}{-p f_p - q f_q} = \frac{dx}{-f_p} = \frac{dy}{-f_q} = \frac{df}{0} $$
Where the subscripts denote partial derivatives.
- Calculate the required partial derivatives
We need to compute the partial derivatives of $f$ with respect to $x, y, z, p,$ and $q$:
$f_x = p$ $f_y = q$ $f_z = -1$ $f_p = x + 2p$ $f_q = y + 2q$
- Substitute the partial derivatives into Charpit's equations
Substituting these into Charpit's equations, we get:
$$ \frac{dp}{p - p} = \frac{dq}{q - q} = \frac{dz}{-p(x+2p) - q(y+2q)} = \frac{dx}{-(x+2p)} = \frac{dy}{-(y+2q)} = \frac{df}{0} $$
- Simplify Charpit's equations
From the first term, we have $\frac{dp}{0} = ...$ and from the second, $\frac{dq}{0} = ...$. This implies that $dp = 0$ and $dq = 0$. Integrating these gives us $p = a$ and $q = b$, where $a$ and $b$ are arbitrary constants.
- Substitute $p$ and $q$ into the original equation
Substitute $p = a$ and $q = b$ into the given equation $Z = px + qy + p^2 + q^2$:
$Z = ax + by + a^2 + b^2$
This represents the complete integral of the given PDE.
$Z = ax + by + a^2 + b^2$
More Information
The complete solution represents a family of planes. Substituting different values for $a$ and $b$ will give different planes that satisfy the given partial differential equation.
Tips
A common mistake is in the calculation of the partial derivatives, so be careful to verify these. Another common mistake is in the manipulation and simplification of Charpit's equations. Also, forgetting the arbitrary constants when integrating $dp=0$ and $dq=0$ is a frequent error.
AI-generated content may contain errors. Please verify critical information