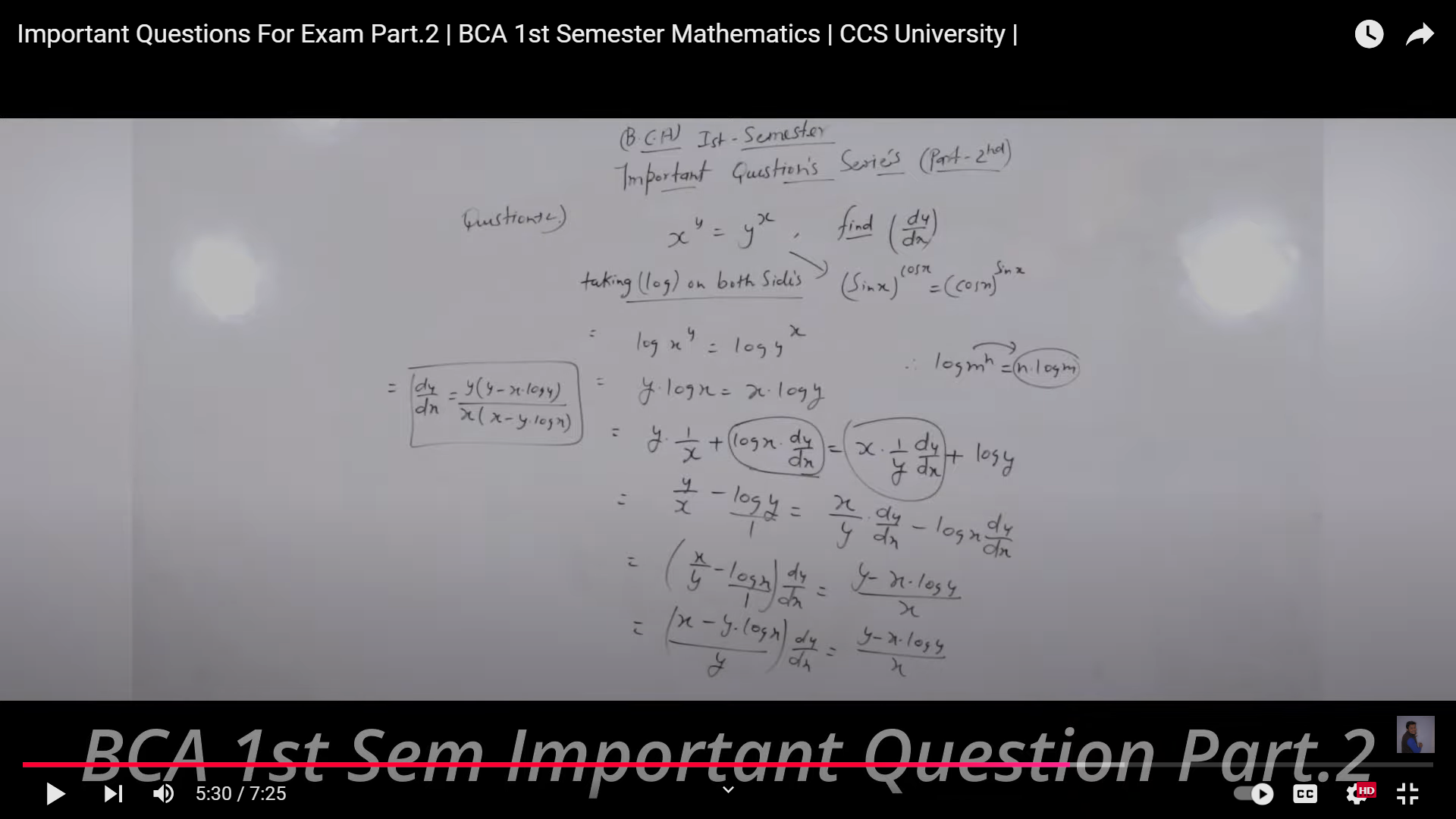
y = x^y, find dy/dn.
Understand the Problem
The question is asking to find the derivative dy/dn of the equation y = x^y using implicit differentiation. This involves taking the logarithm of both sides and applying the rules of differentiation accordingly.
Answer
The derivative \( \frac{dy}{dx} \) is given by: $$ \frac{dy}{dx} = \frac{y^2}{x(1 - y \ln(x))} $$
Answer for screen readers
The derivative ( \frac{dy}{dx} ) is given by: $$ \frac{dy}{dx} = \frac{y^2}{x(1 - y \ln(x))} $$
Steps to Solve
- Take the logarithm on both sides
Start by applying the natural logarithm to both sides of the equation ( y = x^y ): $$ \ln(y) = \ln(x^y) $$
- Apply the power property of logarithms
Using the property of logarithms that allows you to bring the exponent in front: $$ \ln(y) = y \ln(x) $$
- Differentiate both sides with respect to ( x )
Now, differentiate both sides implicitly:
- Left side: $$ \frac{d}{dx}(\ln(y)) = \frac{1}{y} \frac{dy}{dx} $$
- Right side (using the product rule): $$ \frac{d}{dx}(y \ln(x)) = \ln(x) \frac{dy}{dx} + y \frac{1}{x} $$
Putting it all together: $$ \frac{1}{y} \frac{dy}{dx} = \ln(x) \frac{dy}{dx} + \frac{y}{x} $$
- Isolate ( \frac{dy}{dx} )
Now we want to get ( \frac{dy}{dx} ) by itself. Rearranging the equation gives: $$ \frac{1}{y} \frac{dy}{dx} - \ln(x) \frac{dy}{dx} = \frac{y}{x} $$
Factoring out ( \frac{dy}{dx} ): $$ \left( \frac{1}{y} - \ln(x) \right) \frac{dy}{dx} = \frac{y}{x} $$
- Solve for ( \frac{dy}{dx} )
Now solve for ( \frac{dy}{dx} ): $$ \frac{dy}{dx} = \frac{\frac{y}{x}}{\frac{1}{y} - \ln(x)} $$ This can be simplified: $$ \frac{dy}{dx} = \frac{y^2}{x(1 - y \ln(x))} $$
The derivative ( \frac{dy}{dx} ) is given by: $$ \frac{dy}{dx} = \frac{y^2}{x(1 - y \ln(x))} $$
More Information
This problem involves implicit differentiation, which is a technique used when it's difficult to express one variable in terms of another directly. The use of logarithms simplifies the process of differentiation when dealing with exponential forms.
Tips
- Forgetting to apply the product rule correctly when differentiating terms involving ( y ).
- Not remembering to differentiate ( y ) as a function of ( x ), which includes ( \frac{dy}{dx} ) where necessary.
- Misapplying logarithmic properties, such as forgetting that ( \ln(a^b) = b\ln(a) ).
AI-generated content may contain errors. Please verify critical information