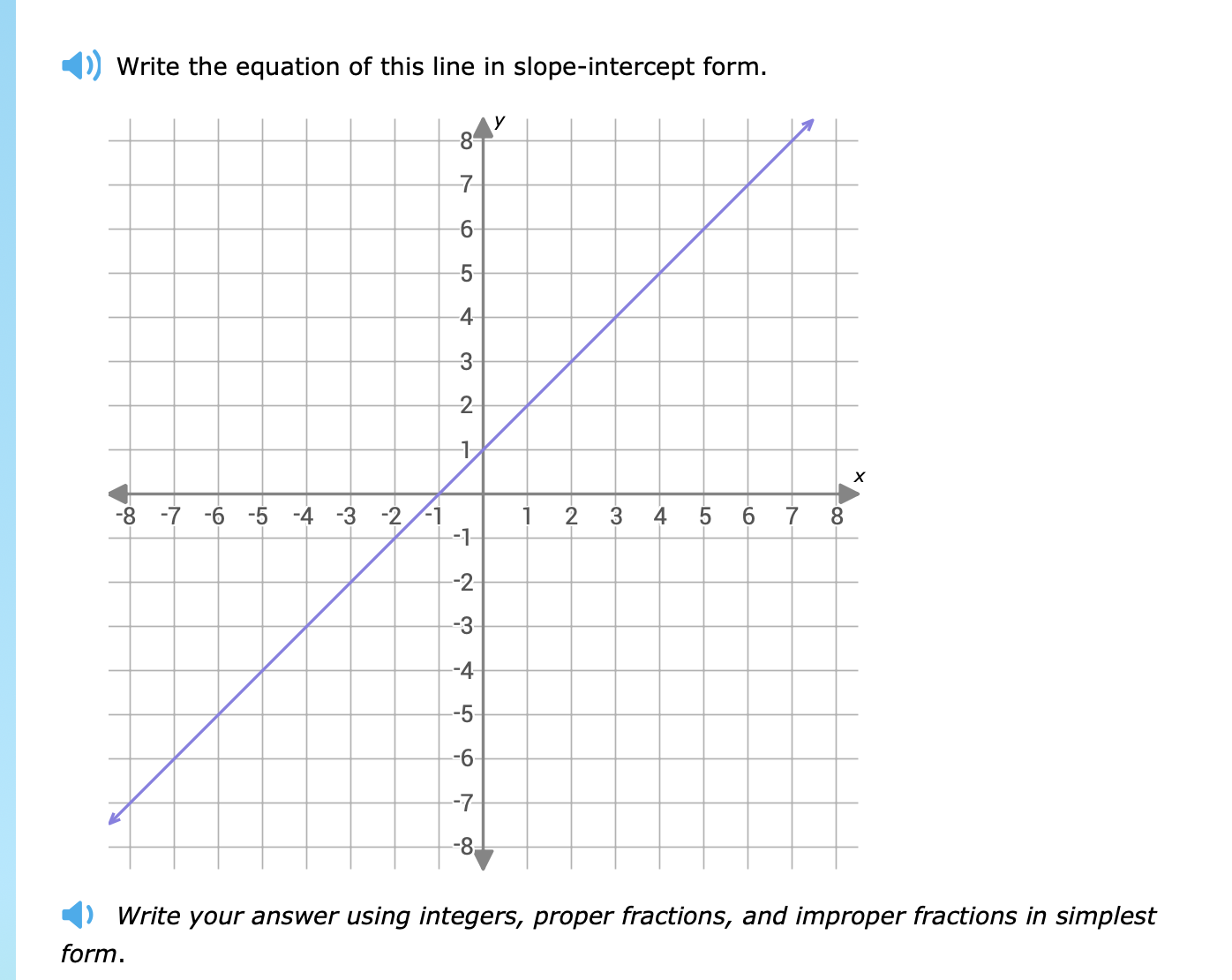
Write the equation of this line in slope-intercept form.
Understand the Problem
The question is asking us to determine the equation of the line shown in the graph in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept. This involves finding the slope and y-intercept from the graph and then writing the equation accordingly.
Answer
The equation of the line is: $y = 2x + 2$.
Answer for screen readers
The equation of the line in slope-intercept form is:
$$ y = 2x + 2 $$
Steps to Solve
- Identify the y-intercept (b)
To find the y-intercept, look at the point where the line crosses the y-axis. From the graph, this line crosses the y-axis at $(0, 2)$. Thus, the y-intercept $b = 2$.
- Determine the slope (m)
The slope $m$ is calculated as the rise over the run between two points on the line. We can select the points $(1, 4)$ and $(2, 6)$ from the graph. The rise from 4 to 6 is $6 - 4 = 2$ and the run from 1 to 2 is $2 - 1 = 1$.
Thus, the slope $m$ can be calculated as: $$ m = \frac{\text{rise}}{\text{run}} = \frac{2}{1} = 2 $$
- Write the equation in slope-intercept form
Now, substitute the values of $m$ and $b$ into the slope-intercept form $y = mx + b$. This gives us: $$ y = 2x + 2 $$
The equation of the line in slope-intercept form is:
$$ y = 2x + 2 $$
More Information
The slope-intercept form is a fundamental concept in algebra, allowing us to express linear equations clearly.
Tips
- Confusing the y-intercept with another point on the line. Always confirm you are using the value where it crosses the y-axis.
- Miscalculating the slope. Ensure you accurately measure the rise and run between points.
AI-generated content may contain errors. Please verify critical information