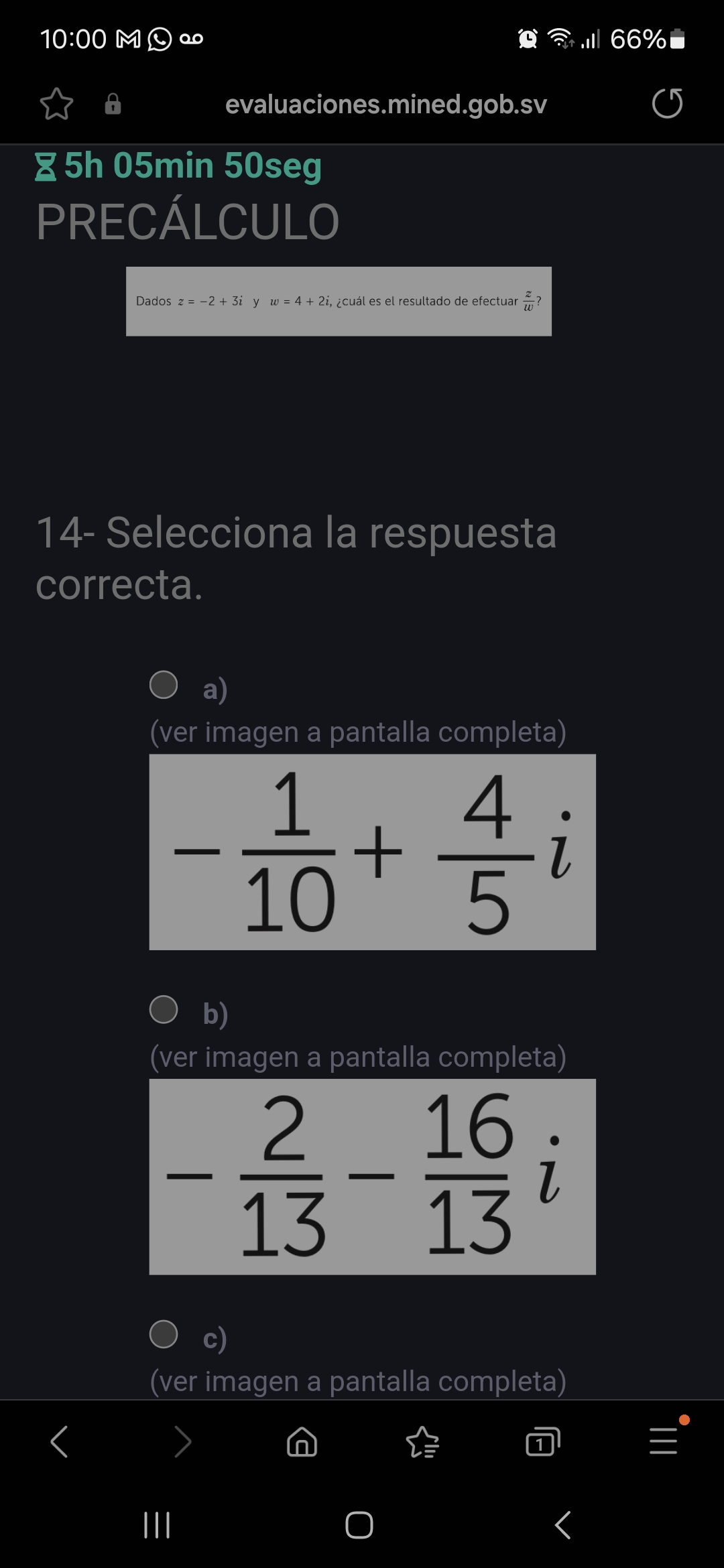
Dados z = -2 + 3i y w = 4 + 2i, ¿cuál es el resultado de efectuar z/w?
Understand the Problem
La pregunta plantea un problema de división de números complejos. Dados dos números complejos, z y w, se pide calcular el resultado de la división z/w y seleccionar la respuesta correcta entre las opciones proporcionadas.
Answer
$-\frac{1}{10} + \frac{4}{5}i$
Answer for screen readers
$-\frac{1}{10} + \frac{4}{5}i$
Steps to Solve
- Substitute the given values of $z$ and $w$ into the expression $\frac{z}{w}$
We have $z = -2 + 3i$ and $w = 4 + 2i$, so we want to find $\frac{-2 + 3i}{4 + 2i}$.
- Multiply the numerator and denominator by the conjugate of the denominator
The conjugate of $4 + 2i$ is $4 - 2i$. Thus, we multiply both the numerator and the denominator by $4 - 2i$: $$ \frac{-2 + 3i}{4 + 2i} \cdot \frac{4 - 2i}{4 - 2i} $$
- Expand the numerator and the denominator
Multiplying the numerator: $$ (-2 + 3i)(4 - 2i) = -2(4) - 2(-2i) + 3i(4) + 3i(-2i) = -8 + 4i + 12i - 6i^2 = -8 + 16i - 6(-1) = -8 + 16i + 6 = -2 + 16i $$
Multiplying the denominator: $$ (4 + 2i)(4 - 2i) = 4(4) + 4(-2i) + 2i(4) + 2i(-2i) = 16 - 8i + 8i - 4i^2 = 16 - 4(-1) = 16 + 4 = 20 $$
- Write the result as a complex number
Now we have: $$ \frac{-2 + 16i}{20} = \frac{-2}{20} + \frac{16i}{20} = -\frac{1}{10} + \frac{4}{5}i $$
$-\frac{1}{10} + \frac{4}{5}i$
More Information
The division of complex numbers involves multiplying the numerator and denominator by the conjugate of the denominator to eliminate the imaginary part from the denominator, resulting in a complex number in the standard form $a + bi$.
Tips
A common mistake is to forget to multiply both the numerator and denominator by the conjugate, or to incorrectly expand the products in the numerator or denominator. Another common mistake is to incorrectly simplify the fraction at the end.
AI-generated content may contain errors. Please verify critical information