Write p^2 - (2p + 1)^2 as a product.
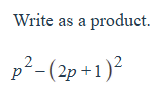
Understand the Problem
The question asks to express the given expression, which is a difference of two squares, as a product. To accomplish this, we will use the difference of squares factorization formula: a^2 - b^2 = (a - b)(a + b). In this context, a is 'p,' and b is '(2p + 1)'. We will substitute these into the formula to determine the product.
Answer
$-(p+1)(3p+1)$
Answer for screen readers
$-(p+1)(3p+1)$
Steps to Solve
-
Apply the difference of squares formula
The difference of squares formula is $a^2 - b^2 = (a - b)(a + b)$. Here, $a = p$ and $b = (2p + 1)$. Substituting these values into the formula, we get: $$p^2 - (2p + 1)^2 = (p - (2p + 1))(p + (2p + 1))$$
-
Simplify the first factor
Simplify the expression inside the first parentheses: $$p - (2p + 1) = p - 2p - 1 = -p - 1 = -(p + 1)$$
-
Simplify the second factor
Simplify the expression inside the second parentheses: $$p + (2p + 1) = p + 2p + 1 = 3p + 1$$
-
Combine the simplified factors
Now, combine the simplified factors to express the original expression as a product: $$p^2 - (2p + 1)^2 = -(p + 1)(3p + 1)$$
$-(p+1)(3p+1)$
More Information
The difference of squares factorization is a useful tool to simplify expressions and solve equations. It's derived from the distributive property.
Tips
A common mistake is not distributing the negative sign correctly when simplifying the first factor $(p - (2p + 1))$. Remember to distribute the negative across both terms inside the parentheses. Another error might occur while simplifying $p + (2p+1)$, it's crucial here to correctly add like terms.
AI-generated content may contain errors. Please verify critical information