Work out the value of fg(6)
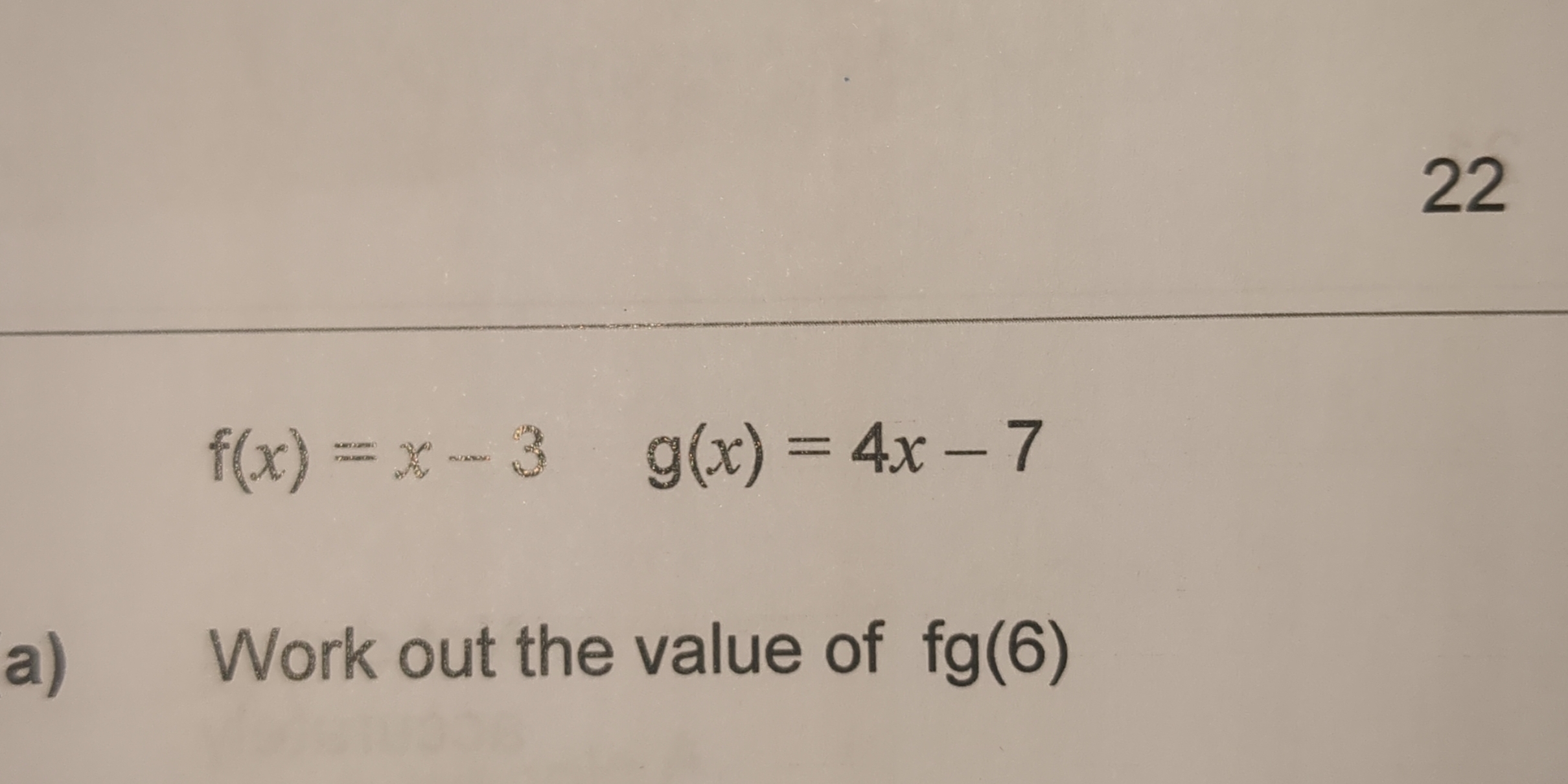
Understand the Problem
The question is asking us to calculate the value of the composite function fg(6), given the definitions of the functions f(x) and g(x). To solve it, we will first find g(6) using its formula and then substitute that result into f(x).
Answer
The value of $fg(6)$ is 14.
Answer for screen readers
The value of $fg(6)$ is 14.
Steps to Solve
-
Calculate g(6)
First, we need to find the value of $g(6)$ by substituting $x = 6$ into the function $g(x)$.
$$ g(6) = 4(6) - 7 $$
This simplifies to:
$$ g(6) = 24 - 7 = 17 $$ -
Calculate f(g(6))
Next, we substitute the result from the previous step into the function $f(x)$ to find $f(g(6)) = f(17)$.
$$ f(17) = 17 - 3 $$
This simplifies to:
$$ f(17) = 14 $$ -
Final Result
Thus, the value of the composite function $fg(6)$ is:
$$ fg(6) = 14 $$
The value of $fg(6)$ is 14.
More Information
Composite functions combine two or more functions where the output of one function becomes the input of another. In this case, we first evaluated $g(6)$ and then used that result to find $f(g(6))$.
Tips
- Forgetting to perform the calculations in the correct order: Always evaluate the inner function first before using its result in the outer function.
- Miscalculating basic arithmetic operations, such as subtraction.
AI-generated content may contain errors. Please verify critical information