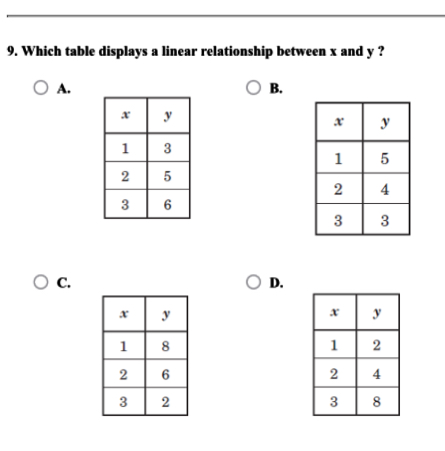
Which table displays a linear relationship between x and y?

Understand the Problem

The question is asking which of the provided tables shows a linear relationship between the variables x and y. A linear relationship can be identified if the change in y is consistent with the change in x across the values in the tables.

Answer

D

Steps to Solve

Identify the change in y for each change in x

For each table, calculate the change in $y$ as $x$ increases:

Table A:
- $1 \to 2$: $3 \to 5$ (change: $2$)
- $2 \to 3$: $5 \to 6$ (change: $1$)
Table B:
- $1 \to 2$: $5 \to 6$ (change: $1$)
- $2 \to 3$: $6 \to 8$ (change: $2$)
Table C:
- $1 \to 2$: $8 \to 3$ (change: $-5$)
- $2 \to 3$: $3 \to 2$ (change: $-1$)
Table D:
- $1 \to 2$: $2 \to 4$ (change: $2$)
- $2 \to 3$: $4 \to 6$ (change: $2$)

Check consistency of changes

A linear relationship means the change in $y$ should be consistent (the same) for equal changes in $x$:

Table A: Changes are inconsistent ($2$, then $1$)
Table B: Changes are inconsistent ($1$, then $2$)
Table C: Changes are inconsistent ($-5$, then $-1$)
Table D: Changes are consistent ($2$, then $2$)

Conclusion based on findings

From the analysis, only Table D shows a consistent change, indicating a linear relationship.

The table that displays a linear relationship between $x$ and $y$ is D.

More Information

Linear relationships imply that as one variable increases, the other increases by a consistent amount. This can often be visualized on a graph as a straight line.

Tips

Assuming consistency without checking all intervals in the table. Always compare the changes across all intervals for accuracy.
Confusing linear relationships with proportional relationships; linear can involve a constant addition or subtraction rather than multiplication.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!