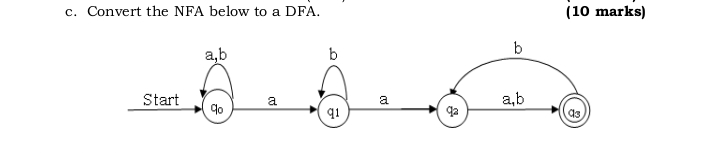
Convert the NFA below to a DFA.
Understand the Problem
The question asks to convert a given Nondeterministic Finite Automaton (NFA) into a Deterministic Finite Automaton (DFA). This requires understanding the states, transitions, and input symbols of the NFA, then constructing a DFA that accepts the same language.
Answer
The DFA is defined by: - States: $\{\{q_0\}, \{q_0, q_1\}, \{q_0, q_1, q_2\}, \{q_0, q_1, q_3\}\}$ - Input alphabet: $\{a, b\}$ - Start state: $\{q_0\}$ - Accepting states: $\{\{q_0, q_1, q_3\}\}$ - Transition function $\delta$ as defined above.
Answer for screen readers
The DFA has the following components:
- States: ${{q_0}, {q_0, q_1}, {q_0, q_1, q_2}, {q_0, q_1, q_3}}$
- Input alphabet: ${a, b}$
- Start state: ${q_0}$
- Accepting states: ${{q_0, q_1, q_3}}$
- Transition function $\delta$ as defined below:
$ \delta({q_0}, a) = {q_0, q_1} $ $ \delta({q_0}, b) = {q_0} $ $ \delta({q_0, q_1}, a) = {q_0, q_1, q_2} $ $ \delta({q_0, q_1}, b) = {q_0, q_1} $ $ \delta({q_0, q_1, q_2}, a) = {q_0, q_1, q_2} $ $ \delta({q_0, q_1, q_2}, b) = {q_0, q_1, q_3} $ $ \delta({q_0, q_1, q_3}, a) = {q_0, q_1, q_2} $ $ \delta({q_0, q_1, q_3}, b) = {q_0, q_1, q_3} $
Steps to Solve
- Identify the NFA's components
The NFA has:
- States: $Q = {q_0, q_1, q_2, q_3}$
- Input alphabet: $\Sigma = {a, b}$
- Start state: $q_0$
- Set of accepting states: $F = {q_3}$
- Transition function: defined by the diagram
- Determine the DFA's start state
The start state of the DFA is the epsilon closure of the start state of the NFA. Since there are no epsilon transitions in the NFA, the start state of the DFA is just ${q_0}$.
- Construct the DFA transition table
We will iteratively determine the DFA's states and transitions.
- Start with the DFA state ${q_0}$.
- Compute transitions for input 'a' and 'b'.
- $ \delta({q_0}, a) = {q_0, q_1} $
- $ \delta({q_0}, b) = {q_0} $
Now we have two DFA states: ${q_0}$ and ${q_0, q_1}$.
- Compute transitions for the state ${q_0, q_1}$.
- $ \delta({q_0, q_1}, a) = {q_0, q_1, q_2} $
- $ \delta({q_0, q_1}, b) = {q_0, q_1} $
Now we have three DFA states: ${q_0}$, ${q_0, q_1}$, and ${q_0, q_1, q_2}$.
- Compute transitions for the state ${q_0, q_1, q_2}$.
- $ \delta({q_0, q_1, q_2}, a) = {q_0, q_1, q_2} $
- $ \delta({q_0, q_1, q_2}, b) = {q_0, q_1, q_3} $
Now we have four DFA states: ${q_0}$, ${q_0, q_1}$, ${q_0, q_1, q_2}$, and ${q_0, q_1, q_3}$.
- Compute transitions for the state ${q_0, q_1, q_3}$.
- $ \delta({q_0, q_1, q_3}, a) = {q_0, q_1, q_2} $
- $ \delta({q_0, q_1, q_3}, b) = {q_0, q_1, q_3} $
Now we have five DFA states: ${q_0}$, ${q_0, q_1}$, ${q_0, q_1, q_2}$, ${q_0, q_1, q_3}$
Since all states transitions lead to already existing states, we are done constructing new states.
- Identify the accepting states in the DFA
Any DFA state that contains an accepting state from the NFA is an accepting state in the DFA. Therefore, ${q_0, q_1, q_3}$ is accepting.
- Summarize the DFA
The DFA has:
- States: ${{q_0}, {q_0, q_1}, {q_0, q_1, q_2}, {q_0, q_1, q_3}}$
- Input alphabet: ${a, b}$
- Start state: ${q_0}$
- Accepting states: ${{q_0, q_1, q_3}}$
- Transition function: as computed above
The DFA has the following components:
- States: ${{q_0}, {q_0, q_1}, {q_0, q_1, q_2}, {q_0, q_1, q_3}}$
- Input alphabet: ${a, b}$
- Start state: ${q_0}$
- Accepting states: ${{q_0, q_1, q_3}}$
- Transition function $\delta$ as defined below:
$ \delta({q_0}, a) = {q_0, q_1} $ $ \delta({q_0}, b) = {q_0} $ $ \delta({q_0, q_1}, a) = {q_0, q_1, q_2} $ $ \delta({q_0, q_1}, b) = {q_0, q_1} $ $ \delta({q_0, q_1, q_2}, a) = {q_0, q_1, q_2} $ $ \delta({q_0, q_1, q_2}, b) = {q_0, q_1, q_3} $ $ \delta({q_0, q_1, q_3}, a) = {q_0, q_1, q_2} $ $ \delta({q_0, q_1, q_3}, b) = {q_0, q_1, q_3} $
More Information
Each state in the resulting DFA corresponds to a set of states from the original NFA, representing all possible states the NFA could be in after reading a particular input string. The accepting states of the DFA are those that include at least one accepting state of the NFA.
Tips
A common mistake is to forget that a DFA state can correspond to a set of NFA states. Another mistake is not correctly calculating the transitions between these sets of states. Forgetting to include all accepting states is another common mistake.
AI-generated content may contain errors. Please verify critical information