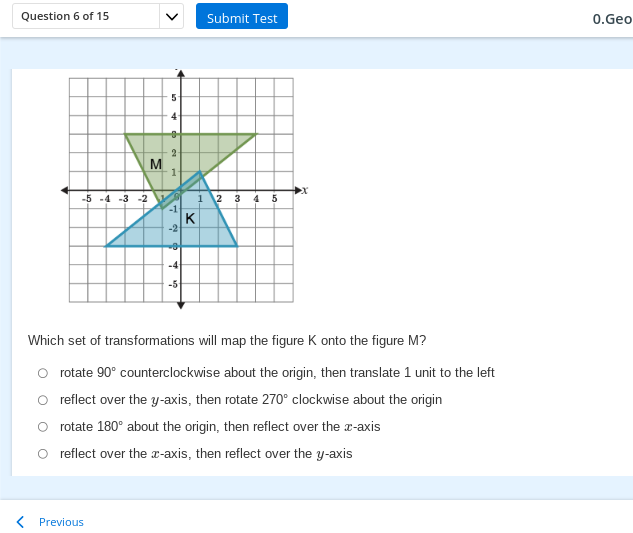
Which set of transformations will map the figure K onto the figure M?

Steps to Solve

1. Identify the Coordinates of Figures K and M

   First, we need to identify the coordinates of the vertices of figure K (the blue triangle) and figure M (the green triangle) from the graph.

   • Figure K has vertices approximately at $(-1, -2)$, $(1, -2)$, and $(0, 1)$.
   • Figure M has vertices approximately at $(-2, 1)$, $(0, 1)$, and $(-1, 4)$.

2. Analyze the Transformations Provided

   We differentiate the effects of each transformation option on figure K:

   1. Rotate 90° counterclockwise about the origin, then translate 1 unit to the left

      This transformation will change the orientation of triangle K and then shift it left.

   2. Reflect over the y-axis, then rotate 270° clockwise about the origin

      Reflecting K will flip it over the y-axis, followed by a clockwise rotation, which also alters its placement.

   3. Rotate 180° about the origin, then reflect over the x-axis

      A 180° rotation moves K to a different quadrant and reflecting it over the x-axis will modify its vertical position.

   4. Reflect over the x-axis, then reflect over the y-axis

      Reflecting over the x-axis flips the triangle down, and the subsequent reflection over the y-axis flips it to the left, potentially returning it to a similar orientation.

3. Test Each Transformation Option

   Evaluate whether each transformation maps figure K onto M.

   • Option 1: Rotate and translate does not achieve the desired position.
   • Option 2: Reflecting K and rotating does not yield the correct positioning.
   • Option 3: This involves possible confirmation that it results in a mapped position close to M.
   • Option 4: This does not give the correct orientation or position.

4. Conclusion

   After testing the transformations, the most viable option that aligns K onto M is option 3.