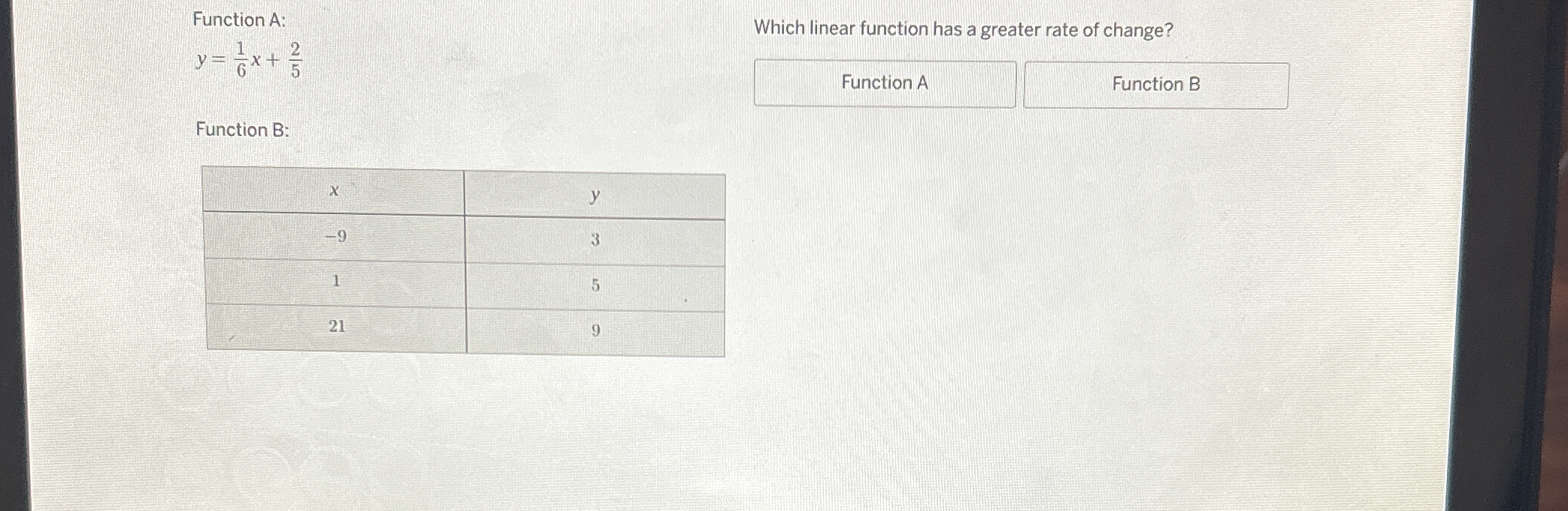
Which linear function has a greater rate of change? Function A: \[y = \frac{1}{6}x + \frac{2}{5}\] Function B: | x | y | | --- | --- | | -9 | 3 | | 1 | 5 | | 21 | 9... Which linear function has a greater rate of change? Function A: \[y = \frac{1}{6}x + \frac{2}{5}\] Function B: | x | y | | --- | --- | | -9 | 3 | | 1 | 5 | | 21 | 9 |
Understand the Problem
The question asks which linear function, A or B, has a greater rate of change. For Function A, you're given the equation, and thus you can directly read off the slope. For Function B, you are given a table of data to estimate the rate of change by picking two points and computing the slope. To arrive at the final answer, you must compare the two slopes.
Answer
Function B
Answer for screen readers
Function B
Steps to Solve
- Find the slope of Function A
The equation of Function A is in the slope-intercept form, $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. From the equation $y = \frac{1}{6}x + \frac{2}{5}$, the slope $m_A$ is $\frac{1}{6}$. $$m_A = \frac{1}{6}$$
- Find the slope of Function B
To find the slope of Function B, we can use two points from the table. Let's use the points $(-9, 3)$ and $(1, 5)$. The slope $m_B$ is given by the formula: $$m_B = \frac{y_2 - y_1}{x_2 - x_1}$$ Plugging in the values, we get: $$m_B = \frac{5 - 3}{1 - (-9)} = \frac{2}{1 + 9} = \frac{2}{10} = \frac{1}{5}$$
- Compare the slopes of Function A and Function B
We have $m_A = \frac{1}{6}$ and $m_B = \frac{1}{5}$. To compare these fractions, we can find a common denominator, which is 30. $$m_A = \frac{1}{6} = \frac{5}{30}$$ $$m_B = \frac{1}{5} = \frac{6}{30}$$ Since $\frac{6}{30} > \frac{5}{30}$, we have $m_B > m_A$.
- Determine which function has a greater rate of change
Since $m_B > m_A$, Function B has a greater rate of change.
Function B
More Information
The rate of change of a linear function is equivalent to its slope. A steeper slope means a greater rate of change in the function.
Tips
- Not correctly identifying the slope from the equation of Function A.
- Incorrectly calculating the slope of Function B using the points from the table (e.g., swapping $x$ and $y$ values or making arithmetic errors).
- Failing to find a common denominator when comparing the slopes, leading to an incorrect conclusion.
AI-generated content may contain errors. Please verify critical information