What scale factor was used to decrease the size of the larger triangle?
Understand the Problem
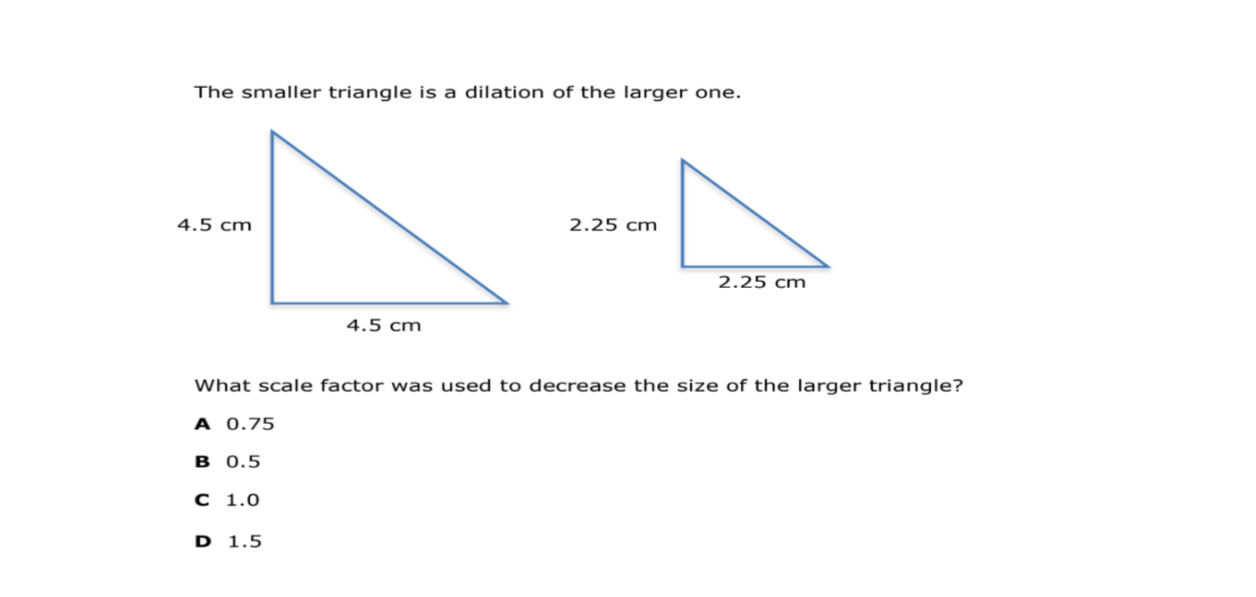
The question presents two similar right triangles, where the smaller triangle is a dilation of the larger one. The side lengths of both triangles are provided. The question asks to determine the scale factor that was used to reduce the size of the larger triangle to create the smaller one. We can calculate the scale factor by dividing a side length of the smaller triangle by the corresponding side length of the larger triangle.
Answer
B 0.5
Answer for screen readers
B 0.5
Steps to Solve
-
Identify corresponding sides We can see that the side with length 4.5 cm in the larger triangle corresponds to the side with length 2.25 cm in the smaller triangle.
-
Calculate the scale factor To find the scale factor, we divide the length of a side in the smaller triangle by the length of the corresponding side in the larger triangle: $$ \text{Scale Factor} = \frac{\text{Length of side in smaller triangle}}{\text{Length of corresponding side in larger triangle}} $$
-
Plug in values and compute $$ \text{Scale Factor} = \frac{2.25}{4.5} = 0.5 $$
B 0.5
More Information
The scale factor of 0.5 means the smaller triangle's sides are half the length of the larger triangle's sides.
Tips
A common mistake is to divide the length of the side in the larger triangle by the length of the side in the smaller triangle. This would give the inverse of the scale factor (i.e. how much larger the bigger triangle is). To avoid this, remember that since the smaller triangle is a reduction of the larger one, the scale factor should be a number less than 1. If the scale factor was greater than 1, the smaller triangle would be an enlargement of the larger triangle.
AI-generated content may contain errors. Please verify critical information