What is the velocity of segment 1?
Understand the Problem
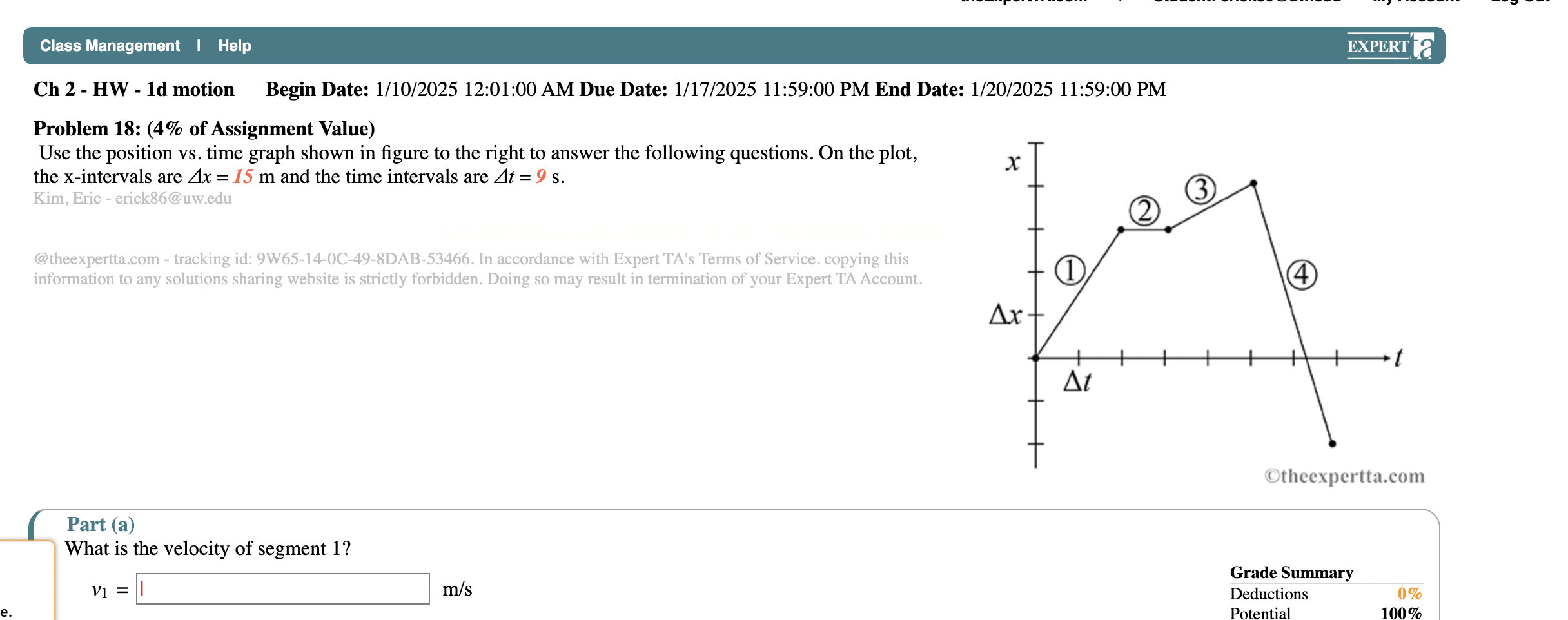
The question is asking for the calculation of the velocity for segment 1 using the provided position vs. time graph. This involves determining the change in position and the change in time during that segment.
Answer
The velocity of segment 1 is approximately $1.67 \, \text{m/s}$.
Answer for screen readers
The velocity of segment 1 is approximately $1.67 , \text{m/s}$.
Steps to Solve
- Identify the values from the graph
From the graph, we know the change in position ($\Delta x$) for segment 1 is given as 15 m. The change in time ($\Delta t$) for segment 1 is given as 9 s.
- Calculate the velocity
The formula for velocity ($v$) is given by:
$$ v = \frac{\Delta x}{\Delta t} $$
Substituting the values into the formula:
$$ v = \frac{15 , \text{m}}{9 , \text{s}} $$
- Perform the division
Now, divide 15 by 9 to find the velocity:
$$ v \approx 1.67 , \text{m/s} $$
The velocity of segment 1 is approximately $1.67 , \text{m/s}$.
More Information
Velocity is a measure of how fast something is moving in a specific direction. In this case, segment 1 has a positive slope, indicating movement in the positive direction.
Tips
- Forgetting to convert units if necessary. Always check that the units for $\Delta x$ and $\Delta t$ match.
- Misreading the values from the graph. Ensure you accurately identify $\Delta x$ and $\Delta t$ from the provided graph.
AI-generated content may contain errors. Please verify critical information