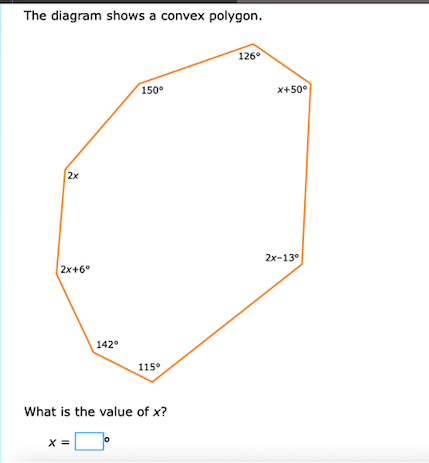
What is the value of x?

Understand the Problem

The question is asking for the value of the variable x in a convex polygon by setting up an equation involving the sum of the interior angles of the polygon. We will need to determine the total sum of the interior angles and set up an equation to solve for x.

Answer

The value of $ x $ is approximately $ 86° $.

Steps to Solve

Determine the number of sides in the polygon

The angles provided indicate that this polygon has 8 sides (octagon), since there are 8 angles given.

Calculate the sum of the interior angles

The formula for the sum of the interior angles of a polygon is given by:

$$ S = (n - 2) \times 180° $$

where ( n ) is the number of sides.

For our polygon:

$$ S = (8 - 2) \times 180° = 6 \times 180° = 1080° $$

Set up the equation for the sum of the angles

Now, we set up the equation by summing all the interior angles:

$$ 150° + 126° + (x + 50°) + (2x) + (2x + 6°) + 142° + 115° + (2x - 13°) = 1080° $$

Combining like terms:

$$ 150° + 126° + 50° + 142° + 115° + 6° - 13° + 7x = 1080° $$

Calculating the constant terms:

$$ 150 + 126 + 50 + 142 + 115 + 6 - 13 = 476 $$

So now we have:

$$ 476 + 7x = 1080 $$

Solve for x

Subtract 476 from both sides:

$$ 7x = 1080 - 476 $$

Simplifying gives:

$$ 7x = 604 $$

Now, divide both sides by 7:

$$ x = \frac{604}{7} $$

Calculating this value results in:

$$ x = 86.2857° $$ (approximately)

Final rounding if necessary

Since angles are typically reported as whole numbers in most contexts, we may round ( x ) to:

$$ x \approx 86° $$

The value of ( x ) is approximately $ 86° $.

More Information

In a convex polygon, the sum of the interior angles must equal ( (n - 2) \times 180° ), which is crucial in determining unknown angle measures. For an octagon, this sum is 1080°.

Tips

Forgetting to convert the polygon from the number of sides to the sum of its interior angles.
Not combining all like terms properly before trying to solve for ( x ).
Miscalculating the sum of constants contributing to the side angles.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!