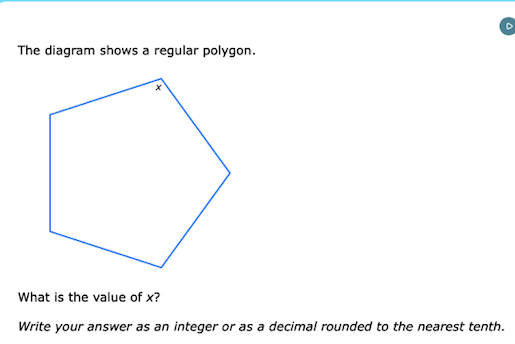
What is the value of x in the diagram of a regular polygon?
Understand the Problem
The question is asking for the value of x in a regular polygon, specifically a pentagon where the angles need to be calculated. We will determine the internal angle of the polygon, which allows us to solve for x.
Answer
$108^\circ$
Answer for screen readers
The value of ( x ) is ( 108^\circ ).
Steps to Solve
- Identify the polygon and its properties
The polygon in question is a regular pentagon, which has 5 equal sides and 5 equal angles.
- Calculate the sum of the interior angles
The formula for the sum of the interior angles of a polygon is given by: $$ \text{Sum of interior angles} = (n - 2) \times 180^\circ $$ where ( n ) is the number of sides. For a pentagon, we have: $$ \text{Sum of interior angles} = (5 - 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ $$
- Find the measure of each interior angle
Since the pentagon is regular, each interior angle is: $$ \text{Interior angle} = \frac{\text{Sum of interior angles}}{n} = \frac{540^\circ}{5} = 108^\circ $$
- Identify the required angle
In the diagram, ( x ) represents the measure of one of the interior angles, which we've calculated to be: $$ x = 108^\circ $$
The value of ( x ) is ( 108^\circ ).
More Information
In a regular pentagon, each interior angle is the same due to its symmetrical properties. Understanding the concept of polygon angles helps in various geometrical problems.
Tips
- Confusing the number of sides of the polygon. Make sure to accurately count the sides.
- Incorrectly applying the formula for the sum of interior angles; remember to subtract 2 from the number of sides ( n ) before multiplying by 180.
AI-generated content may contain errors. Please verify critical information