What is the value of the definite integral of 1/(1+x^3) from 0 to infinity?
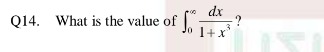
Understand the Problem
The question asks for the value of the definite integral of the function 1/(1+x^3) from 0 to infinity. This requires knowledge of integration techniques, potentially involving partial fractions or other methods to evaluate the integral.
Answer
$\frac{2\pi}{3\sqrt{3}}$
Answer for screen readers
$\frac{2\pi}{3\sqrt{3}}$
Steps to Solve
- Factor the denominator
We start by factoring the denominator $1+x^3$. We know that $a^3 + b^3 = (a+b)(a^2 - ab + b^2)$. Thus, $1 + x^3 = (1+x)(1-x+x^2)$.
- Partial fraction decomposition
We decompose the integrand into partial fractions: $$ \frac{1}{1+x^3} = \frac{1}{(1+x)(1-x+x^2)} = \frac{A}{1+x} + \frac{Bx+C}{1-x+x^2} $$ Multiplying throughout by $1+x^3$ gives $$ 1 = A(1-x+x^2) + (Bx+C)(1+x) $$ $$ 1 = A - Ax + Ax^2 + Bx + Bx^2 + C + Cx $$ $$ 1 = (A+B)x^2 + (-A+B+C)x + (A+C) $$ Comparing the coefficients, we get: $A+B = 0$, $-A+B+C = 0$, $A+C = 1$. Thus $B=-A$ and $C=1-A$. Substituting these into the second equation: $-A - A + 1 - A = 0$, which gives $3A = 1$, so $A = \frac{1}{3}$. Then $B = -\frac{1}{3}$, and $C = 1 - \frac{1}{3} = \frac{2}{3}$.
So our partial fraction decomposition is: $$ \frac{1}{1+x^3} = \frac{1/3}{1+x} + \frac{(-1/3)x + 2/3}{1-x+x^2} = \frac{1}{3} \left( \frac{1}{1+x} + \frac{-x+2}{x^2-x+1} \right) $$
- Integrate each term
We integrate each part separately: $$ \int_{0}^{\infty} \frac{1}{1+x} dx = \left[ \ln(1+x) \right]{0}^{\infty} = \lim{t \to \infty} \ln(1+t) - \ln(1) = \infty $$ However, we need to consider the entire expression: $$ \int_{0}^{\infty} \frac{1}{1+x^{3}} d x=\frac{1}{3} \int_{0}^{\infty} \frac{1}{1+x} d x+\frac{1}{3} \int_{0}^{\infty} \frac{-x+2}{x^{2}-x+1} d x $$ For the second integral, we have: $$ \int_{0}^{\infty} \frac{-x+2}{x^{2}-x+1} d x = -\frac{1}{2} \int_{0}^{\infty} \frac{2 x-1}{x^{2}-x+1} d x+\frac{3}{2} \int_{0}^{\infty} \frac{1}{x^{2}-x+1} d x $$ $$ =-\frac{1}{2} \left[ \ln(x^{2}-x+1) \right]{0}^{\infty}+\frac{3}{2} \int{0}^{\infty} \frac{1}{(x-1/2)^{2}+3/4} d x $$ $$ =-\frac{1}{2} \left[ \ln(x^{2}-x+1) \right]{0}^{\infty} + \frac{3}{2} \cdot \frac{2}{\sqrt{3}} \left[ \arctan\left(\frac{x-1/2}{\sqrt{3}/2}\right) \right]{0}^{\infty} $$ $$ =-\frac{1}{2} \left[ \ln(x^{2}-x+1) \right]{0}^{\infty} + \sqrt{3} \left[ \arctan\left(\frac{2x-1}{\sqrt{3}}\right) \right]{0}^{\infty} $$
- Combine and evaluate the limits
Combining all parts, we get: $$ \frac{1}{3} \left[ \ln(1+x) \right]{0}^{\infty} - \frac{1}{6} \left[ \ln(x^2-x+1) \right]{0}^{\infty} + \frac{\sqrt{3}}{3} \left[ \arctan\left(\frac{2x-1}{\sqrt{3}}\right) \right]{0}^{\infty} $$ $$ =\frac{1}{6} \left[ 2\ln(1+x) - \ln(x^2-x+1) \right]{0}^{\infty} + \frac{\sqrt{3}}{3} \left[ \arctan\left(\frac{2x-1}{\sqrt{3}}\right) \right]{0}^{\infty} $$ $$ =\frac{1}{6} \left[ \ln\left(\frac{(1+x)^2}{x^2-x+1}\right) \right]{0}^{\infty} + \frac{\sqrt{3}}{3} \left[ \arctan\left(\frac{2x-1}{\sqrt{3}}\right) \right]_{0}^{\infty} $$ As $x \to \infty$: $\frac{(1+x)^2}{x^2-x+1} \to \frac{x^2}{x^2} = 1$, so $\ln(1) = 0$. Also $\arctan(\infty) = \frac{\pi}{2}$. At $x=0$: $\ln(\frac{(1+0)^2}{0-0+1}) = \ln(1) = 0$, and $\arctan(\frac{-1}{\sqrt{3}}) = -\frac{\pi}{6}$. Therefore: $$ \frac{1}{6} (0 - 0) + \frac{\sqrt{3}}{3} \left( \frac{\pi}{2} - \left(-\frac{\pi}{6}\right) \right) = \frac{\sqrt{3}}{3} \left( \frac{3\pi+ \pi}{6} \right) = \frac{\sqrt{3}}{3} \cdot \frac{4\pi}{6} = \frac{2\pi\sqrt{3}}{9} = \frac{2\pi}{3\sqrt{3}} $$
$\frac{2\pi}{3\sqrt{3}}$
More Information
The integral $\int_{0}^{\infty} \frac{dx}{1+x^3} = \frac{2\pi}{3\sqrt{3}}$ is a classic example in calculus that showcases integration techniques such as partial fraction decomposition and trigonometric substitution. Alternative methods exist utilizing complex analysis and contour integration.
Tips
A common mistake would be incorrectly applying partial fraction decomposition, especially when dealing with the quadratic term in the denominator. Another mistake could be incorrectly evaluating the limits of the integrated function.
AI-generated content may contain errors. Please verify critical information