What is the value of (f - g)(x) if f(x) = x^3 and g(x) = 4x?
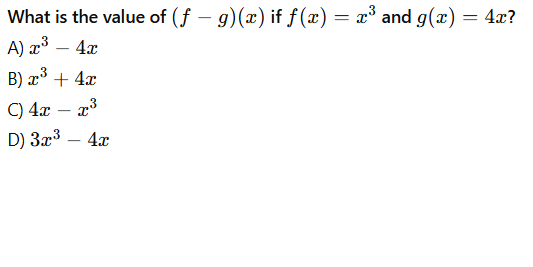
Understand the Problem
The question asks to find the value of (f - g)(x) given the functions f(x) = x^3 and g(x) = 4x. This involves substituting the expressions for f(x) and g(x) into the expression (f - g)(x) and simplifying.
Answer
A) $x^{3} - 4x$
Answer for screen readers
A) $x^{3} - 4x$
Steps to Solve
-
Understand the notation The notation $(f - g)(x)$ means $f(x) - g(x)$.
-
Substitute the expressions for $f(x)$ and $g(x)$ Substitute $f(x) = x^3$ and $g(x) = 4x$ into the expression $f(x) - g(x)$. $f(x) - g(x) = x^3 - 4x$
-
Final Answer Thus, $(f - g)(x) = x^3 - 4x$.
A) $x^{3} - 4x$
More Information
The expression $(f-g)(x)$ represents a new function formed by subtracting the function $g(x)$ from the function $f(x)$.
Tips
A common mistake is to subtract $f(x)$ from $g(x)$ instead of $g(x)$ from $f(x)$, resulting in $4x - x^3$. Also, some might incorrectly combine the terms or perform other algebraic manipulations that are not valid.
AI-generated content may contain errors. Please verify critical information