What is the value of (f - g)(x) if f(x) = x^3 and g(x) = 4x?
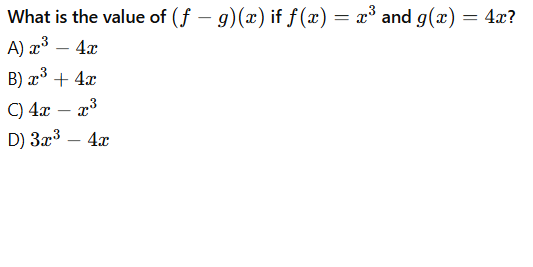
Understand the Problem
The question is asking to find the value of (f - g)(x), given the functions f(x) = x^3 and g(x) = 4x. This involves substituting the given functions into the expression (f - g)(x) and simplifying to find the resulting function.
Answer
A) $x^{3} - 4x$
Answer for screen readers
A) $x^{3} - 4x$
Steps to Solve
- Express (f - g)(x) in terms of f(x) and g(x)
$(f - g)(x)$ means $f(x) - g(x)$.
- Substitute the given functions
Substitute $f(x) = x^3$ and $g(x) = 4x$ into the expression:
$f(x) - g(x) = x^3 - 4x$
- Simplify the expression
The expression $x^3 - 4x$ is already simplified.
A) $x^{3} - 4x$
More Information
The expression $(f-g)(x)$ represents the difference between the two functions $f(x)$ and $g(x)$. It is obtained by subtracting the function $g(x)$ from the function $f(x)$.
Tips
A common mistake is to confuse the order of subtraction, mistakenly calculating $g(x) - f(x)$ instead of $f(x) - g(x)$. Another common mistake is incorrectly performing the subtraction or miscopying the functions.
AI-generated content may contain errors. Please verify critical information