What is the value of (5.0 x 10⁻⁴)(6.0 x 10⁻⁴)/(1.5 x 10³)?
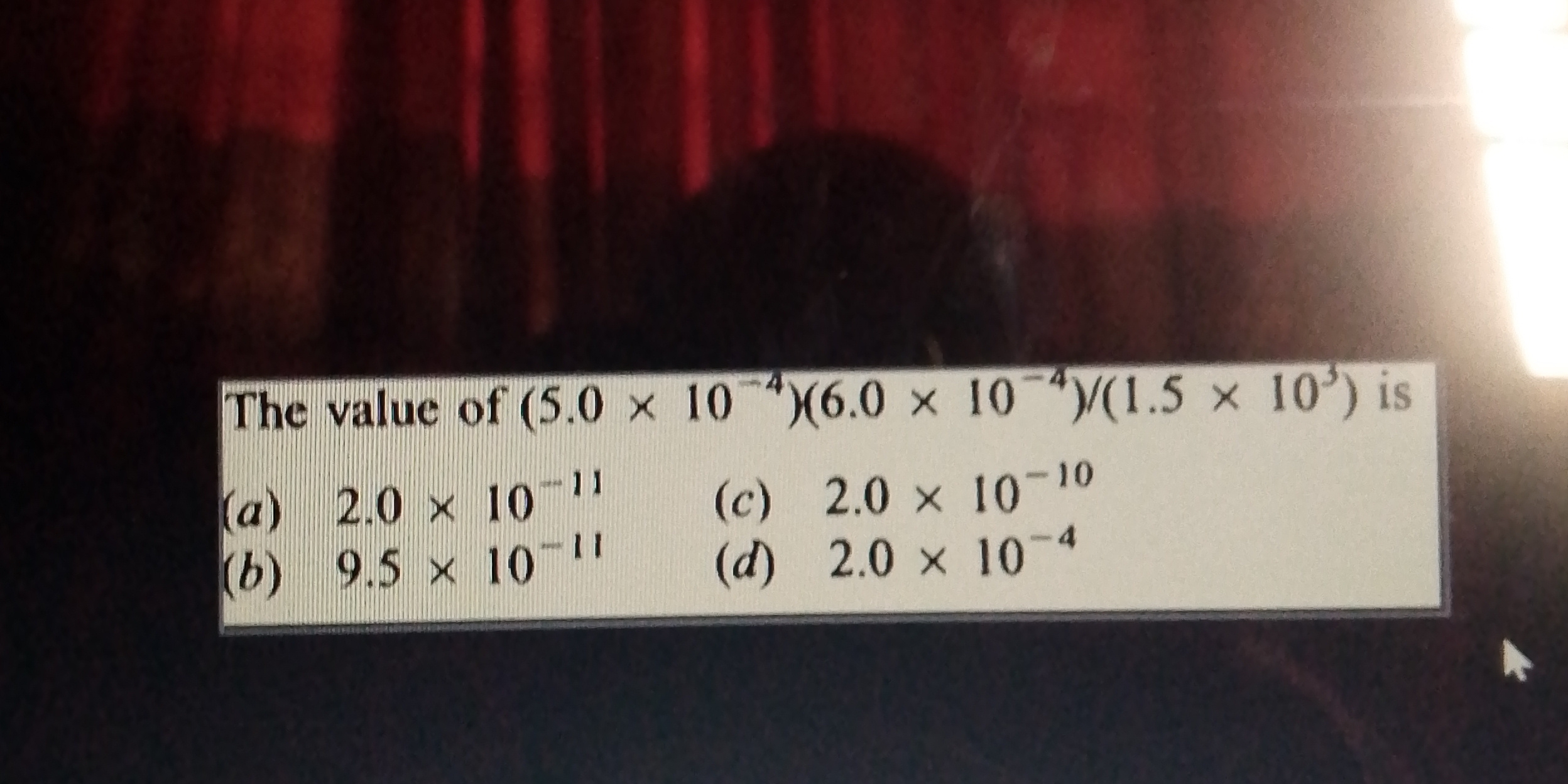
Understand the Problem
The question asks to evaluate the expression (5.0 x 10⁻⁴)(6.0 x 10⁻⁴)/(1.5 x 10³). This involves multiplying and dividing numbers in scientific notation, requiring an understanding of exponent rules.
Answer
$2.0 \times 10^{-10}$
Answer for screen readers
(c) $2.0 \times 10^{-10}$
Steps to Solve
- Multiply the coefficients in the numerator
Multiply the coefficients $5.0$ and $6.0$: $5.0 \times 6.0 = 30.0$
- Multiply the powers of 10 in the numerator
Multiply the powers of $10$ by adding the exponents: $10^{-4} \times 10^{-4} = 10^{-4 + (-4)} = 10^{-8}$
- Rewrite the numerator
Combine the results from steps 1 and 2: $30.0 \times 10^{-8}$
- Divide the coefficient of the numerator by the coefficient of the denominator
Divide $30.0$ by $1.5$: $30.0 / 1.5 = 20.0$
- Divide the powers of 10
Divide the powers of $10$ by subtracting the exponents: $10^{-8} / 10^{3} = 10^{-8 - 3} = 10^{-11}$
- Combine the results
Combine the results from steps 4 and 5: $20.0 \times 10^{-11}$
- Convert to scientific notation
Convert $20.0 \times 10^{-11}$ to proper scientific notation: $20.0 \times 10^{-11} = 2.0 \times 10^{1} \times 10^{-11} = 2.0 \times 10^{1 - 11} = 2.0 \times 10^{-10}$
(c) $2.0 \times 10^{-10}$
More Information
Scientific notation is a way of expressing numbers that are too big or too small to be conveniently written in decimal form. It is commonly used in science and engineering.
Tips
A common mistake is to add the exponents when dividing powers of ten, instead of subtracting them. Another mistake is not converting the final answer to proper scientific notation (where the coefficient is between 1 and 10).
AI-generated content may contain errors. Please verify critical information