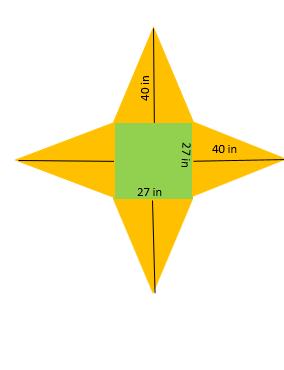
What is the total area of the figure composed of a square with sides of 27 inches and four triangles, each with a base of 27 inches and a height of 40 inches?
Understand the Problem
The question is asking us to calculate the total area of the figure which is composed of a square and four triangles. To solve this, we need to find the area of the square and the area of one triangle, then multiply the triangle's area by four, and finally, add the area of the square and the area of the four triangles.
Answer
2889 square inches
Answer for screen readers
2889 square inches
Steps to Solve
- Calculate the area of the square
The area of a square is side * side. In this case, the side is 27 inches. Area of square = $27 \times 27 = 729$ square inches
- Calculate the area of one triangle
The area of a triangle is $\frac{1}{2} \times base \times height$. In this case, the base is 27 inches and the height is 40 inches. Area of one triangle = $\frac{1}{2} \times 27 \times 40 = 540$ square inches
- Calculate the total area of the four triangles
Since we have 4 identical triangles, we multiply the area of one triangle by 4. Total area of four triangles = $4 \times 540 = 2160$ square inches
- Calculate the total area of the figure
Add the area of the square and the total area of the four triangles. Total area = Area of square + Total area of four triangles Total area = $729 + 2160 = 2889$ square inches
2889 square inches
More Information
The figure is composed of a square and four triangles. By calculating the area of each individual shape and adding them together, we find the figure's total area.
Tips
A common mistake is forgetting to multiply the area of one triangle by four.
AI-generated content may contain errors. Please verify critical information