What is the solution to this system of equations?
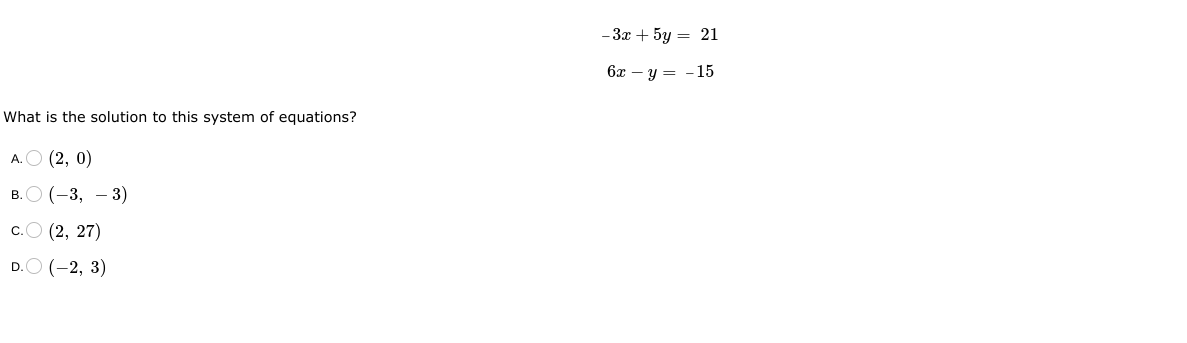
Understand the Problem
The question is asking for the solution to a system of equations. It requires solving for the values of x and y that satisfy both equations given in the image.
Answer
The solution is $(-2, 3)$.
Answer for screen readers
The solution to the system of equations is $(-2, 3)$.
Steps to Solve
-
Identify the equations
The system of equations is:- Equation 1: $-3x + 5y = 21$
- Equation 2: $6x - y = -15$
-
Solve for one variable
Let's solve Equation 2 for $y$.
Rearranging gives us: $$ y = 6x + 15 $$ -
Substitute into the first equation
Now substitute the expression for $y$ from Equation 2 into Equation 1:
$$ -3x + 5(6x + 15) = 21 $$ -
Simplify and solve for $x$
Expanding this gives: $$ -3x + 30x + 75 = 21 $$ Combine like terms: $$ 27x + 75 = 21 $$ Now isolate $x$: $$ 27x = 21 - 75 $$ $$ 27x = -54 $$ $$ x = -2 $$ -
Find $y$ using the value of $x$
Substitute $x = -2$ back into the expression for $y$:
$$ y = 6(-2) + 15 $$ $$ y = -12 + 15 $$ $$ y = 3 $$ -
Solution pairs
The solution to the system of equations is: $$ (x, y) = (-2, 3) $$
The solution to the system of equations is $(-2, 3)$.
More Information
The solution $(-2, 3)$ satisfies both given equations, meaning both equations hold true when these values are substituted back in.
Tips
- Not isolating one variable correctly can lead to errors. Always double-check simplifications.
- Forgetting to substitute the variable back into one of the original equations to find the second variable.
