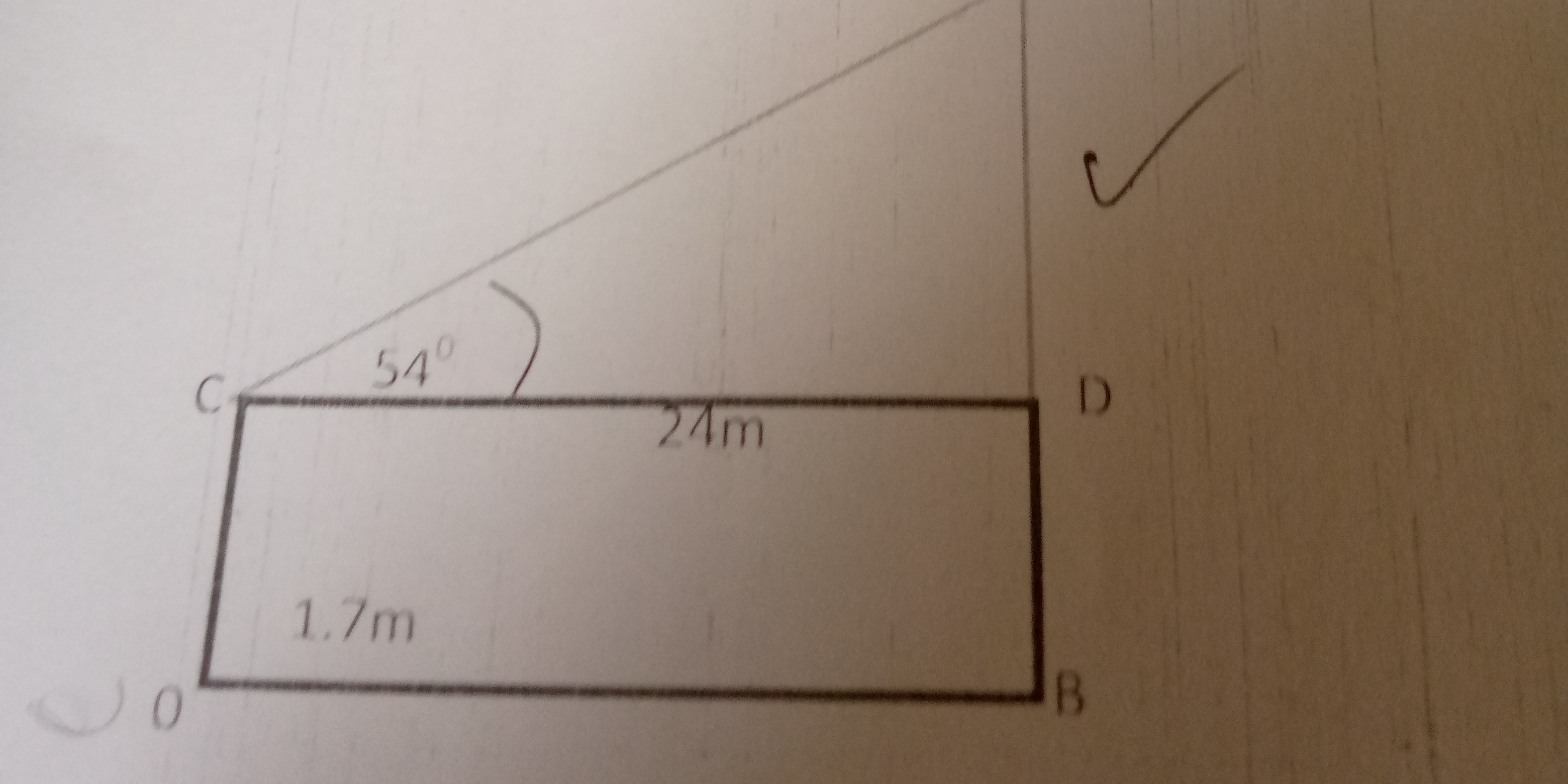
Solve the trigonometry problem on the image.
Understand the Problem
The question involves a geometric figure with given dimensions and an angle. Assuming the goal is is to find the height from the ground to the top of the slanted line, we will calculate the distance BD and then add the 1.7m to find the total height above the ground. The angle provided is at 54 degrees.
Answer
$34.726m$
Answer for screen readers
$34.726m$
Steps to Solve
- Find the length of $BD$ using trigonometry
We are given the length of $CD$ and angle $C$, so we can use the tangent to determine the length of $BD$.
$$tan(54) = \frac{BD}{CD}$$
$$BD = tan(54) \cdot CD$$
$$BD = tan(54) \cdot 24$$
$$BD = 33.026$$
- Find the total height from the ground to the top of the slanted line
The total height from the ground to the top of the slanted line is the sum of the length of $OC$ and $BD$.
$$Total Height = OC + BD$$
$$Total Height = 1.7 + 33.026$$
$$Total Height = 34.726$$
$34.726m$
More Information
The height from the ground to the top of the slanted line is $34.726m$.
Tips
A common mistake is to forget to add the length of $OC$ to the length of $BD$.
AI-generated content may contain errors. Please verify critical information