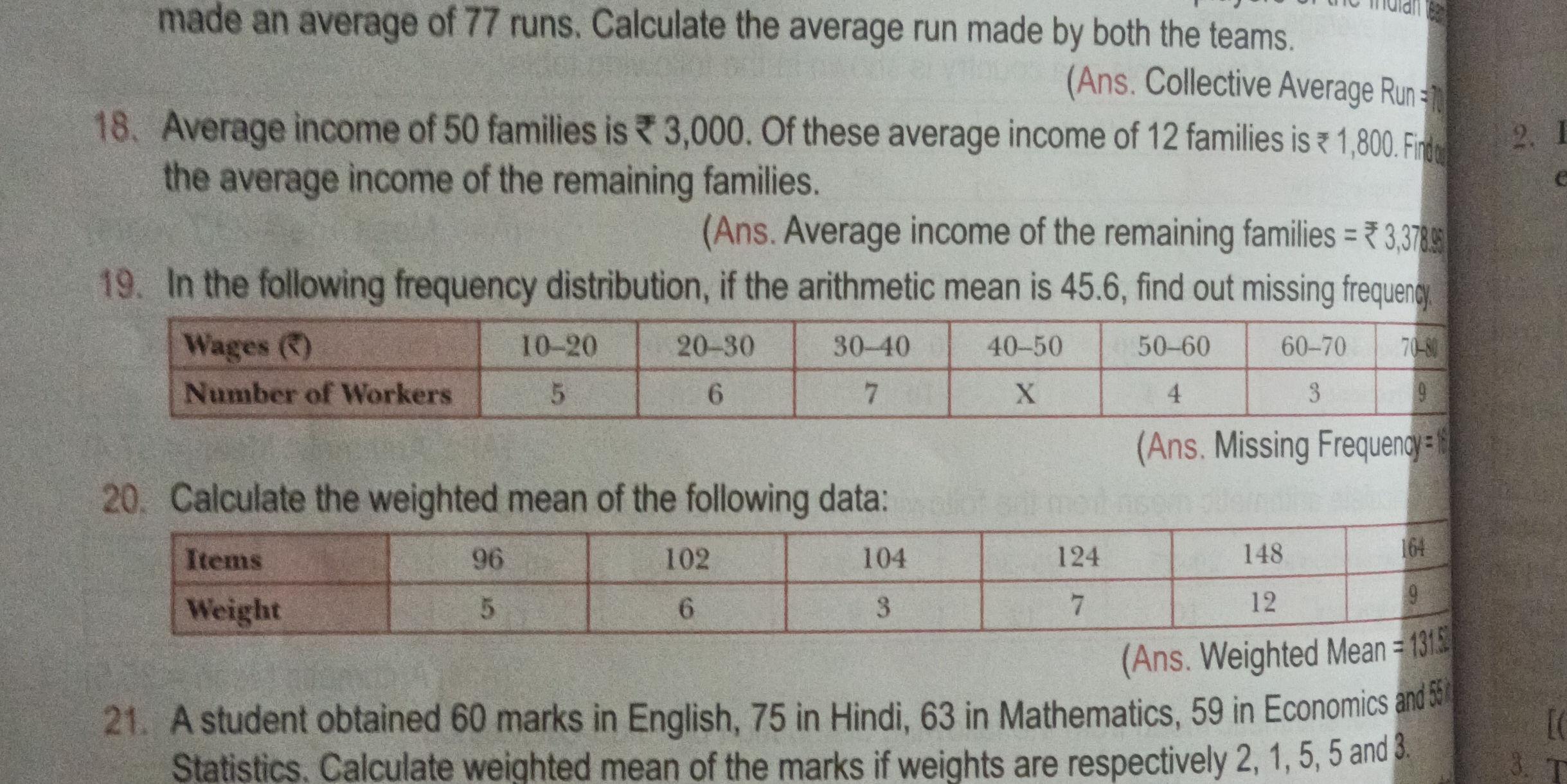
Solve the following math problems: 18. Average income of 50 families is ₹3,000. Of these average income of 12 families is ₹1,800. Find the average income of the remaining families.... Solve the following math problems: 18. Average income of 50 families is ₹3,000. Of these average income of 12 families is ₹1,800. Find the average income of the remaining families. 19. In the following frequency distribution, if the arithmetic mean is 45.6, find out missing frequency. Wages (₹): 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 Number of Workers: 5, 6, 7, X, 4, 3, 9 20. Calculate the weighted mean of the following data: Items: 96, 102, 104, 124, 148, 164 Weight: 5, 6, 3, 7, 12, 9 21. A student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3. Read more

Steps to Solve

Here's how to solve the math problems:

1. Question 18: Find the average income of the remaining families.

   • First, calculate the total income of all 50 families: $50 \times 3000 = 150000$.
   • Then, calculate the total income of the 12 families: $12 \times 1800 = 21600$.
   • Subtract the total income of the 12 families from the total income of the 50 families to find the total income of the remaining families: $150000 - 21600 = 128400$.
   • Find the number of remaining families: $50 - 12 = 38$.
   • Finally, calculate the average income of the remaining families: $128400 / 38 = 3378.95$.

2. Question 19: Find the missing frequency in the frequency distribution.

   • First, find the midpoints of each wage interval: 15, 25, 35, 45, 55, 65, 75.
   • Then, multiply each midpoint by its corresponding frequency: $15 \times 5 = 75$, $25 \times 6 = 150$, $35 \times 7 = 245$, $45 \times X = 45X$, $55 \times 4 = 220$, $65 \times 3 = 195$, $75 \times 9 = 675$.
   • The arithmetic mean is given by the formula: $\text{Mean} = \frac{\sum (\text{Midpoint} \times \text{Frequency})}{\sum \text{Frequency}}$.
   • We know the mean is 45.6, so $45.6 = \frac{75 + 150 + 245 + 45X + 220 + 195 + 675}{5 + 6 + 7 + X + 4 + 3 + 9}$.
   • Simplify the equation: $45.6 = \frac{1560 + 45X}{34 + X}$.
   • Multiply both sides by $(34 + X)$: $45.6(34 + X) = 1560 + 45X$.
   • Expand: $1550.4 + 45.6X = 1560 + 45X$.
   • Subtract $45X$ from both sides: $1550.4 + 0.6X = 1560$.
   • Subtract 1550.4 from both sides: $0.6X = 9.6$.
   • Divide by 0.6: $X = 16$.
   • So, the missing frequency is 16.

3. Question 20: Calculate the weighted mean of the data.

   • Multiply each item by its weight: $96 \times 5 = 480$, $102 \times 6 = 612$, $104 \times 3 = 312$, $124 \times 7 = 868$, $148 \times 12 = 1776$, $164 \times 9 = 1476$.
   • Sum the products: $480 + 612 + 312 + 868 + 1776 + 1476 = 5524$.
   • Sum the weights: $5 + 6 + 3 + 7 + 12 + 9 = 42$.
   • Calculate the weighted mean: $\frac{5524}{42} = 131.52$.

4. Question 21: Calculate the weighted mean of the marks.

   • Multiply each mark by its weight: $60 \times 2 = 120$, $75 \times 1 = 75$, $63 \times 5 = 315$, $59 \times 5 = 295$, $55 \times 3 = 165$.
   • Sum the products: $120 + 75 + 315 + 295 + 165 = 970$.
   • Sum the weights: $2 + 1 + 5 + 5 + 3 = 16$.
   • Calculate the weighted mean: $\frac{970}{16} = 60.625$.