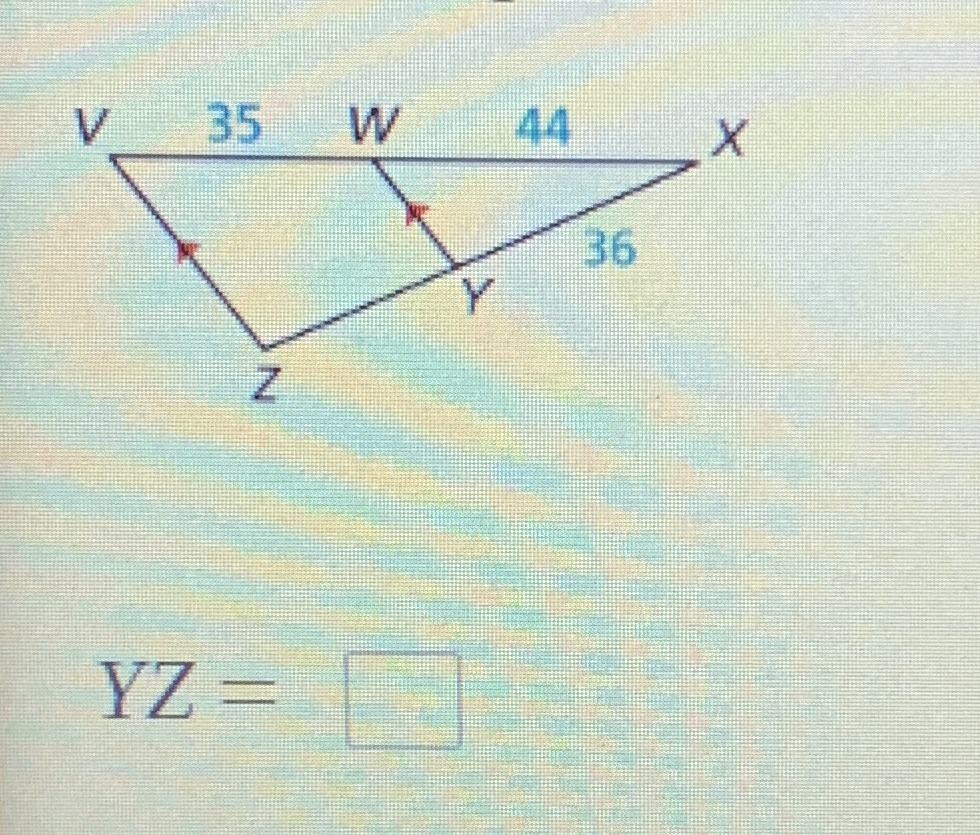
What is the length of YZ?
Understand the Problem
The question is asking to find the length of segment YZ given the lengths of other segments in the figure. The problem involves understanding properties of triangles and possibly using the concept of similar triangles or the triangle side lengths.
Answer
The length of segment $YZ$ is approximately $28.64$.
Answer for screen readers
The length of segment $YZ$ is approximately $28.64$.
Steps to Solve
- Identify similar triangles
In the figure, notice that triangles $VWY$ and $WXZ$ are similar because they share angle $W$ and have one pair of corresponding sides that are equal.
- Set up the proportion using corresponding sides
From the similar triangles, we can establish the following proportion:
$$ \frac{VW}{WX} = \frac{YZ}{XZ} $$
In the given lengths, $VW = 35$, $WX = 44$, and $XZ = 36$. We need to find $YZ$.
- Plug in the known values into the proportion
Using the values we have:
$$ \frac{35}{44} = \frac{YZ}{36} $$
- Cross-multiply to solve for YZ
Cross-multiplying gives:
$$ 35 \cdot 36 = 44 \cdot YZ $$
This leads to:
$$ 1260 = 44 \cdot YZ $$
- Isolate YZ
To find $YZ$, divide both sides by 44:
$$ YZ = \frac{1260}{44} $$
- Simplify the fraction
Calculating that gives:
$$ YZ = 28.6363... $$
Rounding to two decimal places, we have:
$$ YZ \approx 28.64 $$
The length of segment $YZ$ is approximately $28.64$.
More Information
The problem involves properties of similar triangles, where corresponding sides are proportional. This is a fundamental property in geometry used to find unknown lengths when certain relationships are given.
Tips
- Forgetting that triangles must be similar in order to set up the proportion correctly.
- Miscalculating the cross-multiplication step, which can lead to incorrect answers.
- Not simplifying the fractions after calculating the lengths.
AI-generated content may contain errors. Please verify critical information