What is 1 1/2 ÷ 5/6?
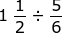
Understand the Problem
The question is asking to divide the mixed fraction 1 1/2 by the fraction 5/6. To solve this, we'll first convert the mixed fraction to an improper fraction, and then multiply by the reciprocal of the second fraction.
Answer
$\frac{9}{5}$
Answer for screen readers
$\frac{9}{5}$ or $1 \frac{4}{5}$
Steps to Solve
- Convert the mixed fraction to an improper fraction
To convert $1 \frac{1}{2}$ to an improper fraction, multiply the whole number (1) by the denominator (2) and add the numerator (1). Then, place the result over the original denominator.
$1 \frac{1}{2} = \frac{(1 \times 2) + 1}{2} = \frac{2 + 1}{2} = \frac{3}{2}$
- Rewrite the division problem
Now we can rewrite the original problem as:
$\frac{3}{2} \div \frac{5}{6}$
- Multiply by the reciprocal
To divide by a fraction, we multiply by its reciprocal. The reciprocal of $\frac{5}{6}$ is $\frac{6}{5}$. So, we have:
$\frac{3}{2} \times \frac{6}{5}$
- Multiply the numerators and the denominators
Multiply the numerators together and the denominators together:
$\frac{3 \times 6}{2 \times 5} = \frac{18}{10}$
- Simplify the fraction
Simplify $\frac{18}{10}$ by dividing both the numerator and denominator by their greatest common divisor, which is 2:
$\frac{18 \div 2}{10 \div 2} = \frac{9}{5}$
- Convert the improper fraction to a mixed fraction (optional)
If desired, convert the improper fraction $\frac{9}{5}$ to a mixed fraction. Divide 9 by 5:
$9 \div 5 = 1$ with a remainder of $4$.
So, $\frac{9}{5} = 1 \frac{4}{5}$
$\frac{9}{5}$ or $1 \frac{4}{5}$
More Information
The result of dividing $1 \frac{1}{2}$ by $\frac{5}{6}$ is $\frac{9}{5}$, which is equivalent to the mixed fraction $1 \frac{4}{5}$.
Tips
A common mistake is forgetting to take the reciprocal of the second fraction when dividing. Remember, dividing by a fraction is the same as multiplying by its reciprocal. Another mistake is incorrectly converting the mixed fraction to an improper fraction. Make sure to multiply the whole number by the denominator and then add the numerator, keeping the same denominator. Also, simplify the fraction to its simplest form at the end of the calculation
AI-generated content may contain errors. Please verify critical information