What is the electric field at point P due to q1 and q2?
Understand the Problem
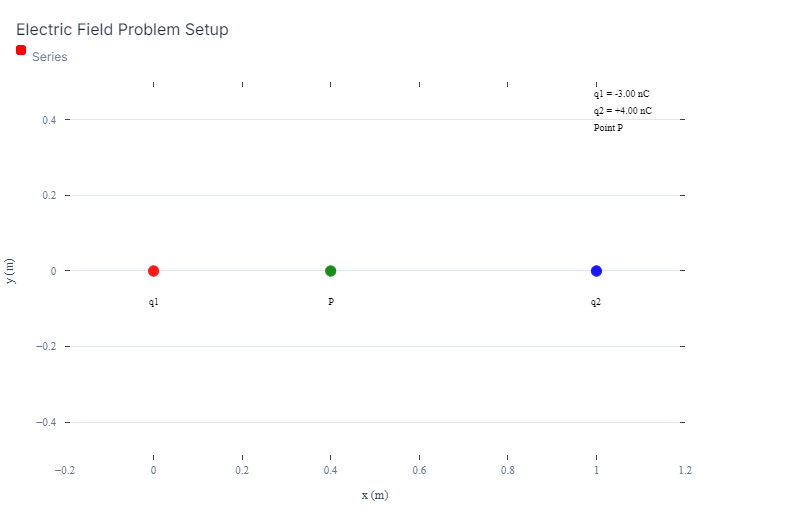
The question is related to calculating the electric field or force at point P due to the charges q1 and q2. It provides a visual setup of the electric field problem but lacks specific details about what needs to be analyzed or calculated.
Answer
The net electric field at point P is calculated by combining the contributions from both charges, given by $E_{\text{net}} = E_1 - E_2$.
Answer for screen readers
The net electric field at point P is given by: $$ E_{\text{net}} = E_1 - E_2 $$
Evaluating this gives a specific numerical value.
Steps to Solve
-
Identify the Charges and Their Positions
We have two charges:
- $q_1 = 3.00 , \text{nC}$ located at position $(0, 0) , \text{m}$
- $q_2 = 4.00 , \text{nC}$ located at position $(1, 0) , \text{m}$ The point P is located at $(0.5, 0) , \text{m}$.
-
Calculate the Distances from Charges to Point P
The distance from $q_1$ to point P is: $$ d_1 = 0.5 , \text{m} $$ The distance from $q_2$ to point P is: $$ d_2 = 0.5 , \text{m} $$
-
Calculate the Electric Field Contributions
The electric field due to a point charge can be calculated using the formula: $$ E = \frac{k \cdot |q|}{r^2} $$ Where ( k \approx 8.99 \times 10^9 , \text{N m}^2/\text{C}^2 ).
For $q_1$: $$ E_1 = \frac{8.99 \times 10^9 \cdot |3.00 \times 10^{-9}|}{(0.5)^2} $$
For $q_2$: $$ E_2 = \frac{8.99 \times 10^9 \cdot |4.00 \times 10^{-9}|}{(0.5)^2} $$
-
Determine the Direction of Each Electric Field
The electric field due to $q_1$ at point P will point away from $q_1$ (to the right), and the electric field due to $q_2$ will point toward $q_2$ (to the left).
-
Calculate the Magnitudes of the Electric Fields
Compute the values: $$ E_1 = \frac{8.99 \times 10^9 \cdot 3.00 \times 10^{-9}}{0.25} $$ $$ E_2 = \frac{8.99 \times 10^9 \cdot 4.00 \times 10^{-9}}{0.25} $$
-
Combine the Electric Fields
Since $E_1$ acts to the right and $E_2$ acts to the left, the net electric field at point P is: $$ E_{\text{net}} = E_1 - E_2 $$
-
Calculate the Final Electric Field Value
Substitute the calculated values of $E_1$ and $E_2$ into the equation to find $E_{\text{net}}$.
The net electric field at point P is given by: $$ E_{\text{net}} = E_1 - E_2 $$
Evaluating this gives a specific numerical value.
More Information
The electric field is a vector quantity that represents the force experienced by a unit charge at a certain point in space due to other charges. The direction of the electric field due to positive charges is away from the charge, and toward for negative charges. The results can help in understanding how electric fields behave in a simple system of point charges.
Tips
- Neglecting sign conventions: Ensure to consider the direction of electric fields correctly based on charge polarity.
- Incorrect distance calculations: Double-check distances to ensure they are measured correctly from the charges to point P.
- Forgetting to square the distance: The formula for the electric field includes the square of the distance, which should not be overlooked.
AI-generated content may contain errors. Please verify critical information