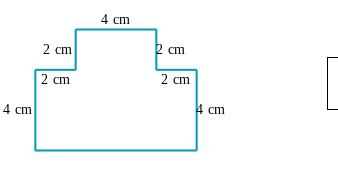
What is the area of the trapezium shown in the image?
Understand the Problem
The question involves calculating the area of a trapezium, which includes identifying its dimensions and applying the necessary formula to find the area.
Answer
The area of the trapezium is \( 24 \text{ cm}^2 \).
Answer for screen readers
The area of the trapezium is ( 24 \text{ cm}^2 ).
Steps to Solve
- Identify the dimensions of the trapezium
The trapezium has two bases: the top base is 4 cm and the bottom base consists of 4 cm plus the two vertical segments (2 cm each on both sides), making it 4 cm + 2 cm + 2 cm = 8 cm.
The height of the trapezium is given as 4 cm.
- Apply the area formula for a trapezium
The area ( A ) of a trapezium can be calculated using the formula:
$$ A = \frac{1}{2} \times (b_1 + b_2) \times h $$
where ( b_1 ) and ( b_2 ) are the lengths of the two bases, and ( h ) is the height.
- Substitute the values into the formula
Substituting the values into the area formula:
- ( b_1 = 4 ) cm
- ( b_2 = 8 ) cm
- ( h = 4 ) cm
This gives us:
$$ A = \frac{1}{2} \times (4 + 8) \times 4 $$
- Calculate the area
First, calculate the sum of the bases:
$$ 4 + 8 = 12 $$
Now substitute back into the area formula:
$$ A = \frac{1}{2} \times 12 \times 4 $$
Now perform the multiplication:
$$ A = 6 \times 4 = 24 \text{ cm}^2 $$
The area of the trapezium is ( 24 \text{ cm}^2 ).
More Information
Trapeziums (or trapezoids in some regions) can sometimes be tricky, especially in terms of identifying the bases and height. This is a classic calculation found often in geometry problems.
Tips
- Confusing bases: Ensure to identify the top and bottom bases correctly.
- Miscalculating the total length of the bottom base: Remember to account for additional segments on the trapezium shape.
AI-generated content may contain errors. Please verify critical information