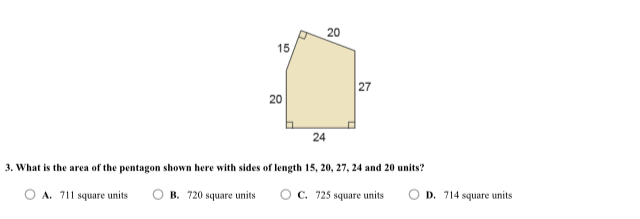
What is the area of the pentagon shown here with sides of length 15, 20, 27, 24 and 20 units?

Steps to Solve

1. Divide the pentagon into a rectangle and a right triangle

Draw a horizontal line from the top left vertex (where the sides of length 15 and 20 meet) to the right side of the pentagon. This splits the pentagon into a rectangle at the bottom and a right triangle at the top.

2. Find the dimensions of the rectangle

The rectangle has sides of length 24 (base) and 20 (height).

3. Calculate the area of the rectangle

The area of a rectangle is base times height. $Area_{rectangle} = 24 \times 20 = 480$

4. Find the dimensions of the right triangle

The height of the triangle is given as 15. The base of the triangle is the difference between the total height 27 and the height of the rectangle 20, so its height is $27 - 20 = 7$

5. Calculate the area of the right triangle

The area of a right triangle is $\frac{1}{2} \times base \times height = \frac{1}{2} \times 24 \times 7 = 84$

Note: the base of the triangle is $24-20 = 4$. So $ \frac{1}{2} \times 4 \times 15 = 30.$

6. Find the dimensions of the triangle on the left The triangle on the left has base 4 and height 15, using the side length dimensions

7. Determine the combined area

Sum the area of the rectangle and the triangle.$Area = 480 + 30 = 510$