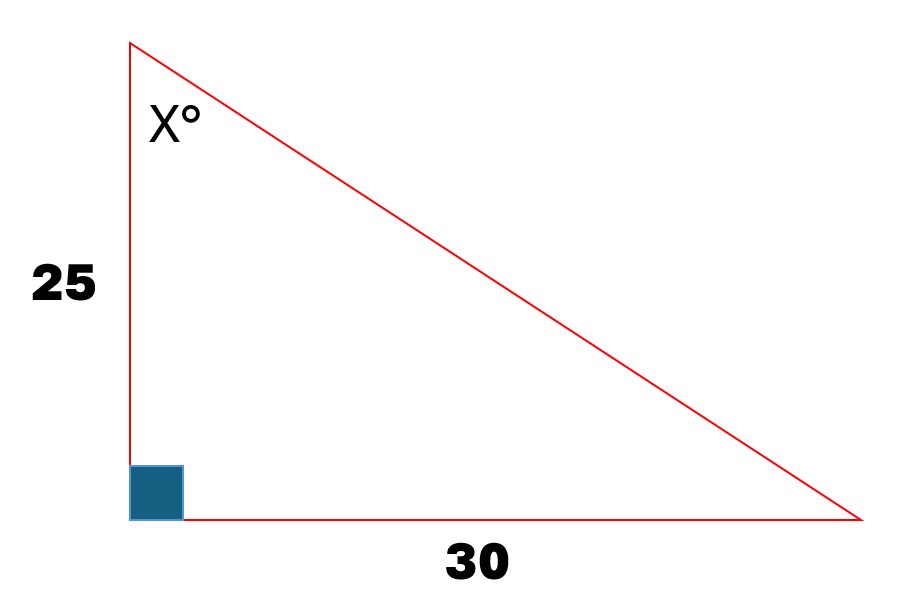
What is the angle X in the right triangle with sides of length 25 and 30?
Understand the Problem
The question involves a right triangle with one side measuring 25 and the other side measuring 30, and it is asking to find the angle X° opposite the side with a length of 25.
Answer
The angle \(X\) is approximately \(40.601^\circ\).
Answer for screen readers
The angle (X) is approximately (40.601^\circ).
Steps to Solve
- Identify the triangle properties
In a right triangle, the sides are related to the angles through trigonometric functions. We have the opposite side (25) and the adjacent side (30).
- Use the tangent function
To find the angle (X^\circ), we can use the tangent function, which is defined as the ratio of the opposite side to the adjacent side:
$$ \tan(X) = \frac{\text{opposite}}{\text{adjacent}} = \frac{25}{30} $$
- Calculate the angle
Now, we take the arctangent (inverse tangent) to find the angle (X):
$$ X = \tan^{-1}\left(\frac{25}{30}\right) $$
- Compute using a calculator
Calculating the above expression using a calculator:
$$ X = \tan^{-1}\left(\frac{25}{30}\right) \approx 40.601^\circ $$
The angle (X) is approximately (40.601^\circ).
More Information
The tangent function relates the angles and sides of a right triangle, allowing for easy calculation of angles when the lengths of two sides are known. This concept is useful in many real-world applications, including architecture and engineering.
Tips
- Confusing the sides: Ensure you correctly identify which side is opposite and which is adjacent to the angle in question.
- Using the wrong function: Remember to use the tangent function for opposite and adjacent sides. Using sine or cosine inappropriately can lead to incorrect results.
