Solve the following system of equations: 2x - 7y = 31 3x + 5y = -31
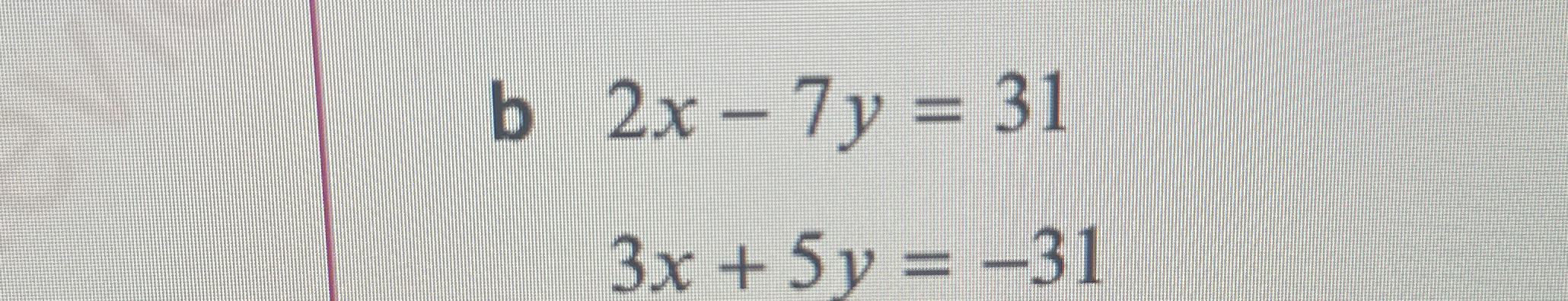
Understand the Problem
The question provides a system of two linear equations in two variables (x and y). The task is to solve this system, which typically involves finding the values of x and y that satisfy both equations simultaneously. Common methods include substitution, elimination, or using matrices.
Answer
$x = -2$, $y = -5$
Answer for screen readers
$x = -2$, $y = -5$
Steps to Solve
-
Label the equations Let's label the given equations: Equation 1: $2x - 7y = 31$ Equation 2: $3x + 5y = -31$
-
Multiply equations to prepare for elimination We'll use the method of elimination. Multiply Equation 1 by 3 and Equation 2 by 2, so the coefficients of $x$ will be the same: $3 \times (2x - 7y) = 3 \times 31 \implies 6x - 21y = 93$ $2 \times (3x + 5y) = 2 \times (-31) \implies 6x + 10y = -62$
-
Eliminate x and solve for y Subtract the second modified equation from the first one to eliminate $x$: $(6x - 21y) - (6x + 10y) = 93 - (-62)$ $6x - 21y - 6x - 10y = 93 + 62$ $-31y = 155$ $y = \frac{155}{-31}$ $y = -5$
-
Substitute y back into one of the original equations to solve for x Substitute $y = -5$ into Equation 1: $2x - 7(-5) = 31$ $2x + 35 = 31$ $2x = 31 - 35$ $2x = -4$ $x = \frac{-4}{2}$ $x = -2$
-
Solution The solution to the system of equations is $x = -2$ and $y = -5$.
$x = -2$, $y = -5$
More Information
We found the solution to the system of equations by using the elimination method. We multiplied the equations by constants so we can obtain the same $x$ coefficient and eliminate the $x$ variable.
Tips
A common mistake is to make errors during the multiplication or subtraction steps when eliminating variables. Careful attention to signs is crucial. Also, after finding the value of one variable, some students might forget to substitute it back into one of the original equations to find the value of the other variable.
AI-generated content may contain errors. Please verify critical information