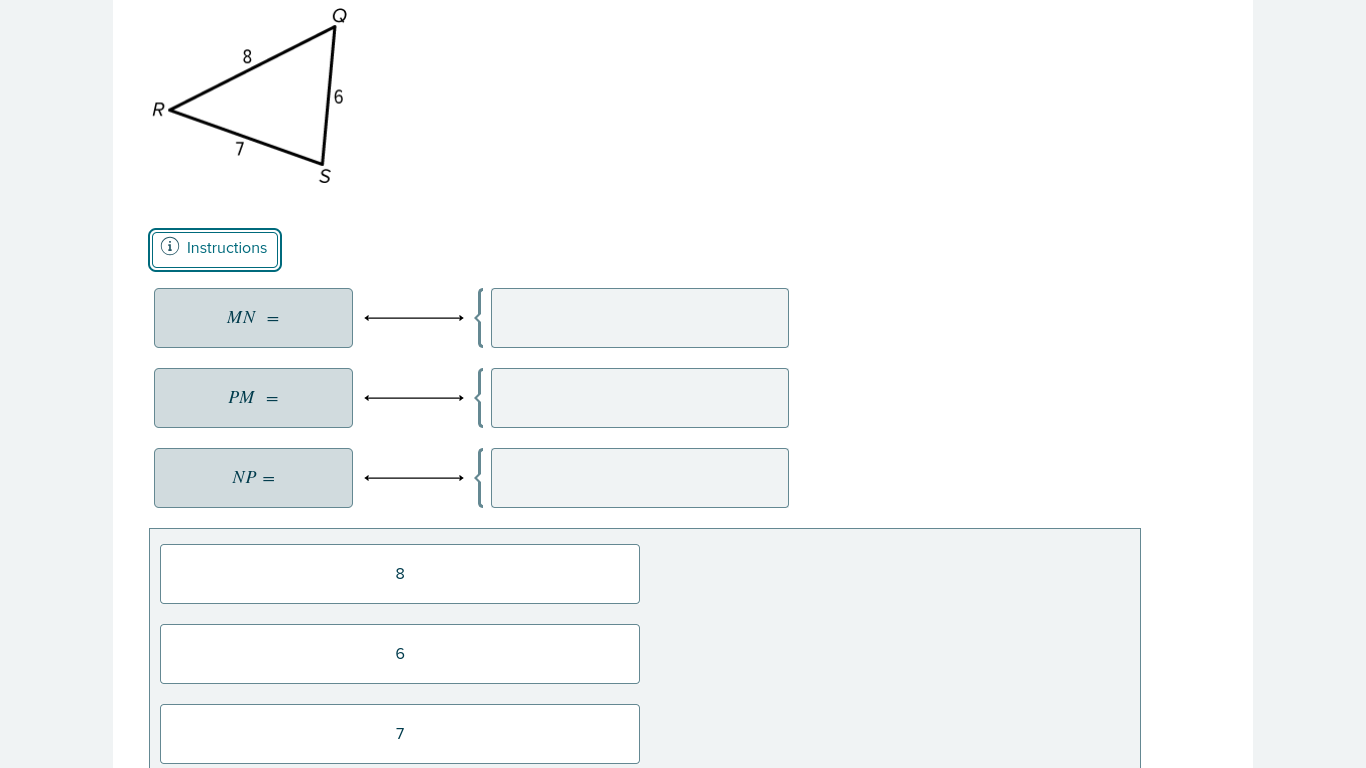
What are the lengths of MN, PM, and NP in the given triangle?

Understand the Problem

The question is asking for the values of segments MN, PM, and NP based on a triangle with given side lengths. To solve this, we would typically use the properties of triangles, possibly involving segment lengths and geometric relationships.

Answer

$MN = 8, PM = 6, NP = 7$

Steps to Solve

Identify Known Values We have a triangle ( QRS ) with side lengths: ( QR = 8 ), ( RS = 6 ), and ( QS = 7 ).
Use the Triangle Segment Ratio Theorem From the triangle segment ratio theorem, if ( M ), ( N ), and ( P ) divide ( QR ), ( RS ), and ( QS ) respectively in specific ratios, we can find segments ( MN ), ( PM ), and ( NP ).
Apply the Ratio Assuming the segments are proportionally divided, we will use the triangle's sides:

Let ( MN ) correspond to the ratio of the segments dividing ( QR ).
Let ( PM ) correspond to the ratio of the segments dividing ( RS ).
Let ( NP ) correspond to the ratio of the segments dividing ( QS ).

Calculate Segment Lengths Using ( QR ), ( RS ), and ( QS ):

( MN = \text{Length associated with } QR)
( PM = \text{Length associated with } RS)
( NP = \text{Length associated with } QS)

Assuming segment lengths are direct representations of numbers as given:

( MN = 8 )
( PM = 6 )
( NP = 7 )

( MN = 8 )
( PM = 6 )
( NP = 7 )

More Information

These lengths correspond to the segments of the triangle based on a direct relationship with the triangle's side lengths. This is often used in geometry to simplify calculations and understand geometric properties.

Tips

Null

AI-generated content may contain errors. Please verify critical information

Thank you for voting!