Use the matrix method to solve the following: x + 2y + 3z = 20, 3x - 6y + 2z = 32, x + y + z = 9.
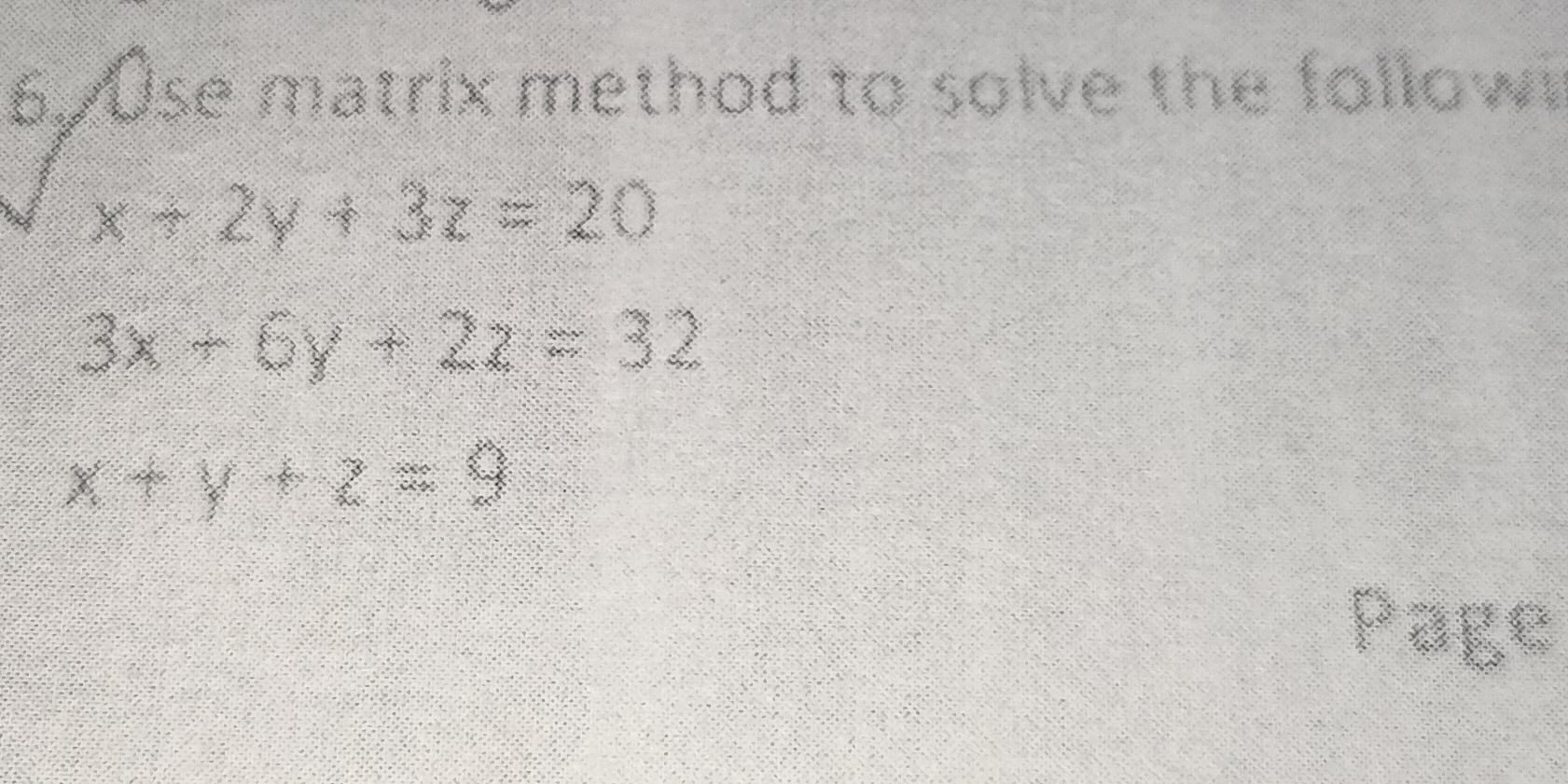
Understand the Problem
The question is asking to use the matrix method to solve a system of linear equations. The equations given are in standard form, and we need to apply matrix techniques to find the values of x, y, and z.
Answer
$$ x = -\frac{135}{17}, \quad y = -\frac{43}{17}, \quad z = \frac{72}{17} $$
Answer for screen readers
The solution to the system of equations is: $$ x = -\frac{135}{17}, \quad y = -\frac{43}{17}, \quad z = \frac{72}{17} $$
Steps to Solve
- Set up the matrix equations
Convert the system of equations into matrix form $AX = B$, where $$ A = \begin{bmatrix} 1 & 2 & 3 \ 3 & -6 & 2 \ 1 & 1 & 1 \end{bmatrix}, \quad X = \begin{bmatrix} x \ y \ z \end{bmatrix}, \quad B = \begin{bmatrix} 20 \ 32 \ 9 \end{bmatrix} $$
- Find the inverse of matrix A
Calculate the determinant of matrix $A$ to check if it is invertible: $$ \text{det}(A) = 1(-6 \cdot 1 - 2 \cdot 1) - 2(3 \cdot 1 - 2 \cdot 1) + 3(3 \cdot 1 - (-6) \cdot 1) $$ Calculating gives: $$ = 1(-6 - 2) - 2(3 - 2) + 3(3 + 6) = -8 - 2 + 27 = 17 $$
Since the determinant is not zero, $A$ is invertible.
- Calculate the inverse of A
Use the formula for the inverse of a 3x3 matrix. After finding the cofactors and transposing, we get $$ A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix} -4 & -2 & 1 \ -1 & -1 & 1 \ 2 & 1 & 0 \end{bmatrix} $$ Thus, $$ A^{-1} = \frac{1}{17} \begin{bmatrix} -4 & -2 & 1 \ -1 & -1 & 1 \ 2 & 1 & 0 \end{bmatrix} $$
- Multiply A^{-1} with B
Now, compute $X = A^{-1}B$: $$ X = A^{-1} \begin{bmatrix} 20 \ 32 \ 9 \end{bmatrix} = \frac{1}{17} \begin{bmatrix} -4 & -2 & 1 \ -1 & -1 & 1 \ 2 & 1 & 0 \end{bmatrix} \begin{bmatrix} 20 \ 32 \ 9 \end{bmatrix} $$
Carrying out the multiplication: $$ X = \frac{1}{17} \begin{bmatrix} -4(20) - 2(32) + 1(9) \ -1(20) - 1(32) + 1(9) \ 2(20) + 1(32) + 0(9) \end{bmatrix} $$
Calculating the elements gives: $$ = \frac{1}{17} \begin{bmatrix} -80 - 64 + 9 \ -20 - 32 + 9 \ 40 + 32 + 0 \end{bmatrix} = \frac{1}{17} \begin{bmatrix} -135 \ -43 \ 72 \end{bmatrix} $$
- Final values
Calculate final values: $$ X = \begin{bmatrix} \frac{-135}{17} \ \frac{-43}{17} \ \frac{72}{17} \end{bmatrix} $$
Thus, $$ x = -\frac{135}{17}, \quad y = -\frac{43}{17}, \quad z = \frac{72}{17} $$
The solution to the system of equations is: $$ x = -\frac{135}{17}, \quad y = -\frac{43}{17}, \quad z = \frac{72}{17} $$
More Information
The matrix method is a systematic way to solve systems of linear equations by transforming them into a format using matrices and their inverses. This method is particularly useful for larger systems.
Tips
- Forgetting to check if the matrix is invertible by calculating the determinant.
- Miscomputing the inverse of the matrix.
- Errors during matrix multiplication, especially in signs and calculations.
AI-generated content may contain errors. Please verify critical information