Use the equation $x^2 + \frac{1}{x^2} = 5$ to evaluate the expression $(x + \frac{1}{x})^2$.
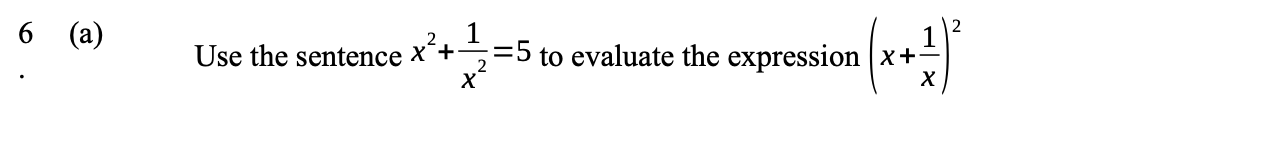
Understand the Problem
The question asks to evaluate the expression $(x + \frac{1}{x})^2$ given that $x^2 + \frac{1}{x^2} = 5$. To solve this, we can expand the expression and try to relate it to the given equation.
Answer
$ (x + \frac{1}{x})^2 = 7 $
Answer for screen readers
$ (x + \frac{1}{x})^2 = 7 $
Steps to Solve
-
Expand the expression Expand the expression $(x + \frac{1}{x})^2$ using the formula $(a+b)^2 = a^2 + 2ab + b^2$: $$ (x + \frac{1}{x})^2 = x^2 + 2(x)(\frac{1}{x}) + (\frac{1}{x})^2 = x^2 + 2 + \frac{1}{x^2} $$
-
Rearrange the terms Rearrange the terms to group $x^2$ and $\frac{1}{x^2}$ together: $$ (x + \frac{1}{x})^2 = x^2 + \frac{1}{x^2} + 2 $$
-
Substitute the given value Substitute the given value $x^2 + \frac{1}{x^2} = 5$ into the equation: $$ (x + \frac{1}{x})^2 = 5 + 2 $$
-
Simplify Simplify the expression to find the final value: $$ (x + \frac{1}{x})^2 = 7 $$
$ (x + \frac{1}{x})^2 = 7 $
More Information
The problem demonstrates how algebraic manipulation and substitution can be used to evaluate expressions without explicitly solving for the variable $x$.
Tips
A common mistake is to incorrectly expand $(x + \frac{1}{x})^2$. Remember to include the cross term $2(x)(\frac{1}{x}) = 2$. Some might also try to solve for $x$ from $x^2 + \frac{1}{x^2} = 5$, which is unnecessary and more complicated.
AI-generated content may contain errors. Please verify critical information