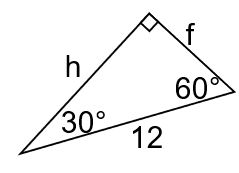
In the triangle with dimensions 12, 30°, and 60°, find the height (h) and side (f).

Steps to Solve

1. Identify the right triangle configuration

In a right triangle with angles of 30° and 60°, we can label the sides based on the known angle and the given length. The side opposite the 30° angle will be the smallest and can be denoted as $h$, while the side opposite the 60° angle will be the longer side denoted as $f$.

2. Use sine to find height (h)

The sine function relates the angle to the opposite side over the hypotenuse. Here, we can use the formula

$$ \sin(30^\circ) = \frac{h}{12} $$

Since $ \sin(30^\circ) = \frac{1}{2} $, we have:

$$ \frac{1}{2} = \frac{h}{12} $$

Now, multiply both sides by 12 to isolate $h$:

$$ h = 12 \times \frac{1}{2} = 6 $$

3. Use cosine to find side (f)

Next, we can find the length of side $f$ using the cosine function, which relates the angle to the adjacent side over the hypotenuse:

$$ \cos(30^\circ) = \frac{f}{12} $$

Since $ \cos(30^\circ) = \frac{\sqrt{3}}{2} $, we have:

$$ \frac{\sqrt{3}}{2} = \frac{f}{12} $$

Now, multiply both sides by 12 to solve for $f$:

$$ f = 12 \times \frac{\sqrt{3}}{2} = 6\sqrt{3} $$