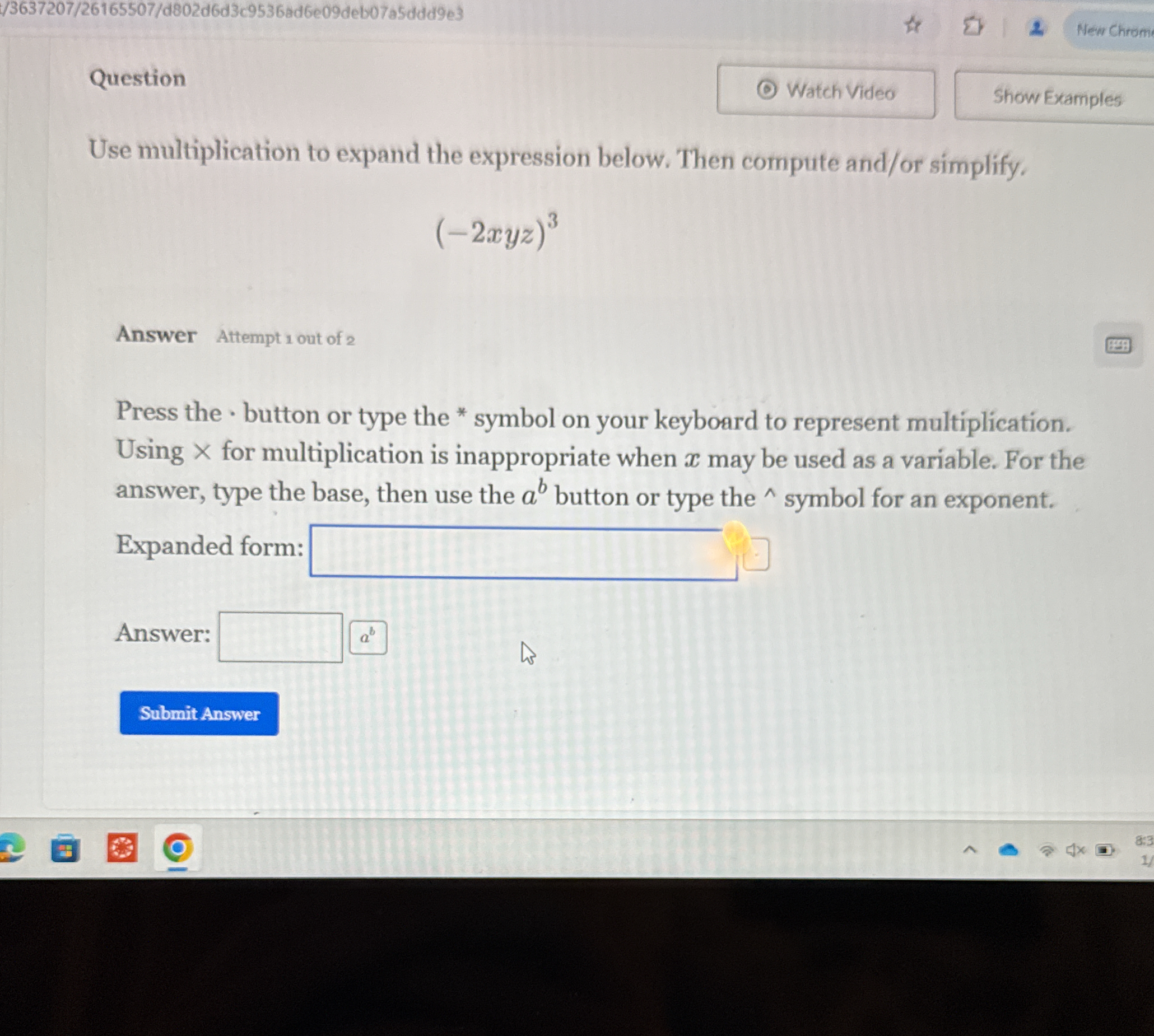
Use multiplication to expand the expression below. Then compute and/or simplify. (-2xyz)³
Understand the Problem
The question is asking to expand the expression (-2xyz) raised to the power of 3 using multiplication, and then compute and/or simplify it.
Answer
The expanded form is $-8x^3y^3z^3$.
Answer for screen readers
The expanded form of $(-2xyz)^3$ is $-8x^3y^3z^3$.
Steps to Solve
- Identify the Expression to Expand
We need to expand the expression $(-2xyz)^3$.
- Expand Using Definition of Exponents
The expression can be expanded using the definition of exponents, which states that $(a \cdot b)^n = a^n \cdot b^n$. Here, we can apply the exponent to each part of the product:
$$ (-2)^3 \cdot (x)^3 \cdot (y)^3 \cdot (z)^3 $$
- Calculate Each Component
Now we compute each part:
- Calculate $(-2)^3$:
$$ (-2)^3 = -8 $$
- The variables raise to the power of 3:
$$ (x)^3 = x^3, \quad (y)^3 = y^3, \quad (z)^3 = z^3 $$
- Combine All the Components
Now we can put everything together:
$$ -8 \cdot x^3 \cdot y^3 \cdot z^3 $$
- Final Expanded Form
Thus, the expanded form of the expression is:
$$ -8x^3y^3z^3 $$
The expanded form of $(-2xyz)^3$ is $-8x^3y^3z^3$.
More Information
When expanding expressions with negative coefficients raised to a power, remember that the negative sign retains its value when the exponent is odd (like 3 in this case). If the exponent were even, the negative sign would become positive.
Tips
- Forgetting to apply the exponent to each variable.
- Miscalculating negative numbers raised to odd/even powers.
- Not multiplying coefficients properly.
AI-generated content may contain errors. Please verify critical information