Factorise: y^2 - 10y + 21
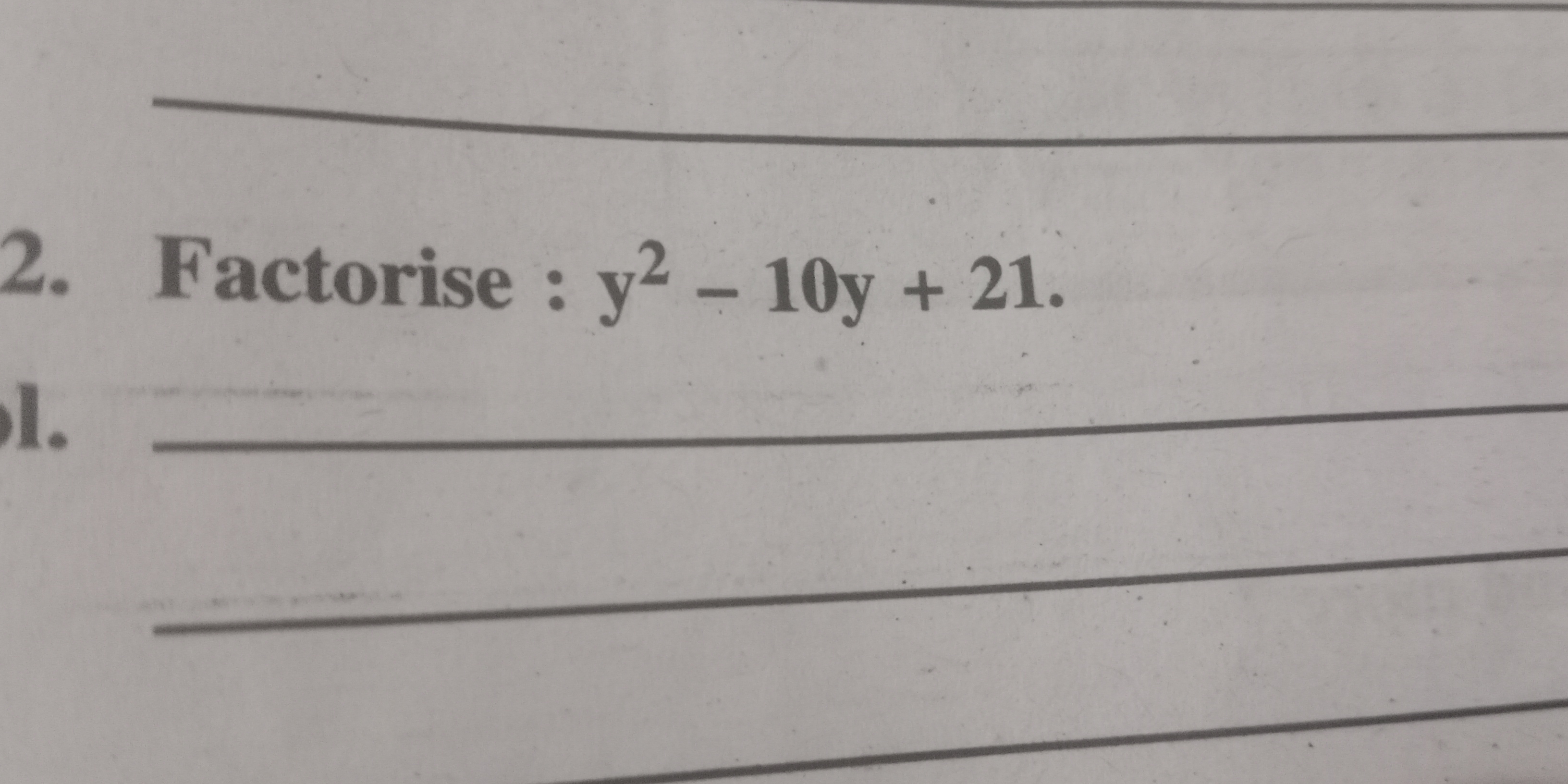
Understand the Problem
The question asks to factorise the quadratic expression y^2 - 10y + 21. This involves finding two binomials that, when multiplied together, give the original quadratic expression.
Answer
$(y - 3)(y - 7)$
Answer for screen readers
$(y - 3)(y - 7)$
Steps to Solve
- Identify the coefficients
The quadratic expression is in the form $ay^2 + by + c$, where $a = 1$, $b = -10$, and $c = 21$.
- Find two numbers that multiply to $c$ and add up to $b$
We need to find two numbers that multiply to 21 and add up to -10. These two numbers are -3 and -7, since $(-3) \times (-7) = 21$ and $(-3) + (-7) = -10$.
- Write the factorised form
Using the numbers found in the previous step, we can write the factorised form as $(y - 3)(y - 7)$.
$(y - 3)(y - 7)$
More Information
When you multiply $(y - 3)(y - 7)$, you should get back the original quadratic expression, $y^2 - 10y + 21$.
Tips
A common mistake is to get the signs wrong when finding the two numbers that multiply to $c$ and add to $b$. For instance, choosing 3 and 7 instead of -3 and -7 would lead to an incorrect factorisation. Always double-check that the numbers satisfy both conditions (multiplication and addition).
AI-generated content may contain errors. Please verify critical information