Use a table to find the product of ( rac{1}{5}d - 12)(-7 + rac{5}{4}d).
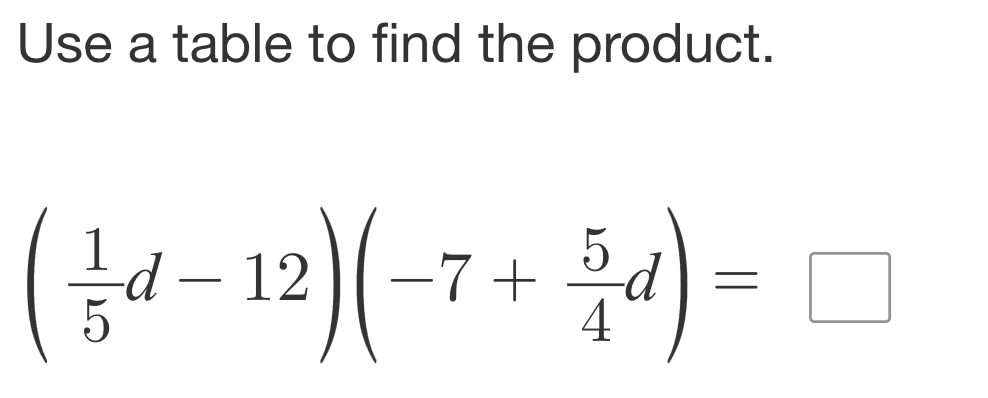
Understand the Problem
The question asks to find the product of two binomials: ( rac{1}{5}d - 12) and (-7 + rac{5}{4}d). You need to use a table (likely referring to a multiplication table or the box method) to organize and multiply each term of the first binomial by each term of the second binomial, then simplify the result by combining like terms.
Answer
$\frac{1}{4}d^2 - \frac{82}{5}d + 84$
Answer for screen readers
$\frac{1}{4}d^2 - \frac{82}{5}d + 84$
Steps to Solve
- Set up the table (box method)
Create a 2x2 table. Label the rows with the terms of the first binomial $(\frac{1}{5}d - 12)$ and the columns with the terms of the second binomial $(-7 + \frac{5}{4}d)$.
| -7 | $\frac{5}{4}d$ | |
|---|---|---|
| $\frac{1}{5}d$ | ||
| -12 |
- Multiply each term and fill in the table
Multiply each term of the first binomial with each term of the second binomial and write the result in the corresponding cell.
- $(\frac{1}{5}d) \cdot (-7) = -\frac{7}{5}d$
- $(\frac{1}{5}d) \cdot (\frac{5}{4}d) = \frac{1}{4}d^2$
- $(-12) \cdot (-7) = 84$
- $(-12) \cdot (\frac{5}{4}d) = -15d$
Fill the table:
| -7 | $\frac{5}{4}d$ | |
|---|---|---|
| $\frac{1}{5}d$ | $-\frac{7}{5}d$ | $\frac{1}{4}d^2$ |
| -12 | 84 | -15d |
- Write out the expression
Write out the product as the sum of the terms in the table:
$\frac{1}{4}d^2 - \frac{7}{5}d - 15d + 84$
- Combine like terms
Combine the 'd' terms: $-\frac{7}{5}d - 15d$. To do this, find a common denominator, which is 5.
$-\frac{7}{5}d - \frac{75}{5}d = -\frac{82}{5}d$
- Write the final expression
Substitute the combined term back into the expression:
$\frac{1}{4}d^2 - \frac{82}{5}d + 84$
$\frac{1}{4}d^2 - \frac{82}{5}d + 84$
More Information
The box method helps to organize the multiplication of binomials, ensuring that each term is multiplied by every other term correctly.
Tips
- Sign Errors: Be careful with negative signs when multiplying.
- Incorrect Multiplication of Fractions: Ensure the numerators and denominators are multiplied correctly.
- Forgetting to Combine Like Terms: Failing to simplify the expression after multiplication.
- Incorrectly Combining Like Terms: Make sure that like terms (terms with the same variable and exponent) are correctly combined by adding or subtracting their coefficients.
AI-generated content may contain errors. Please verify critical information