The solutions to the equation x³ + 4x² + x - 2 = 0 are -1, A, and B. What is the value of A² + B²?
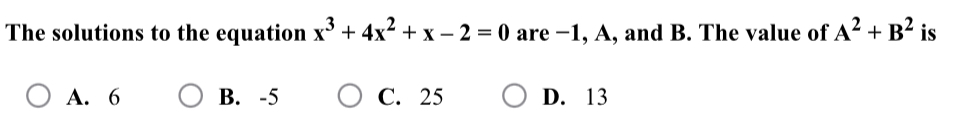
Understand the Problem
The question asks us to find the roots of the cubic equation x³ + 4x² + x - 2 = 0. One root is given as -1, so we need to find the other two roots (A and B), and then calculate A² + B².
Answer
13
Answer for screen readers
13
Steps to Solve
- Polynomial Division
Since we know that $x = -1$ is a root of the polynomial $x^3 + 4x^2 + x - 2 = 0$, then $(x + 1)$ must be a factor. We can perform polynomial division to find the other factor.
$$(x^3 + 4x^2 + x - 2) \div (x + 1)$$
- Performing the Division
Dividing $x^3 + 4x^2 + x - 2$ by $x + 1$, we obtain $x^2 + 3x - 2$.
- Quadratic Equation
So, we have $x^3 + 4x^2 + x - 2 = (x + 1)(x^2 + 3x - 2) = 0$. Since we already know the root from the factor $(x + 1)$, we solve the quadratic equation: $$x^2 + 3x - 2 = 0$$
- Quadratic Formula
Use the quadratic formula to find the roots $A$ and $B$: $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ Where $a = 1$, $b = 3$, and $c = -2$: $$x = \frac{-3 \pm \sqrt{3^2 - 4(1)(-2)}}{2(1)}$$ $$x = \frac{-3 \pm \sqrt{9 + 8}}{2}$$ $$x = \frac{-3 \pm \sqrt{17}}{2}$$ So, the roots are $A = \frac{-3 + \sqrt{17}}{2}$ and $B = \frac{-3 - \sqrt{17}}{2}$.
- Calculate $A^2 + B^2$ $$A^2 = \left(\frac{-3 + \sqrt{17}}{2}\right)^2 = \frac{9 - 6\sqrt{17} + 17}{4} = \frac{26 - 6\sqrt{17}}{4}$$ $$B^2 = \left(\frac{-3 - \sqrt{17}}{2}\right)^2 = \frac{9 + 6\sqrt{17} + 17}{4} = \frac{26 + 6\sqrt{17}}{4}$$ $$A^2 + B^2 = \frac{26 - 6\sqrt{17}}{4} + \frac{26 + 6\sqrt{17}}{4} = \frac{26 - 6\sqrt{17} + 26 + 6\sqrt{17}}{4} = \frac{52}{4} = 13$$
13
More Information
The roots of the cubic equation are $-1$, $\frac{-3 + \sqrt{17}}{2}$, and $\frac{-3 - \sqrt{17}}{2}$. The sum of squares of the non -1 roots is 13.
Tips
A common mistake is miscalculating the squares of the roots when calculating $A^2$ and $B^2$. For example, forgetting to square both the numerator and denominator, or incorrectly simplifying the expression $(\frac{-3 \pm \sqrt{17}}{2})^2$. Another common mistake is making an error while dividing the polynomial.
AI-generated content may contain errors. Please verify critical information