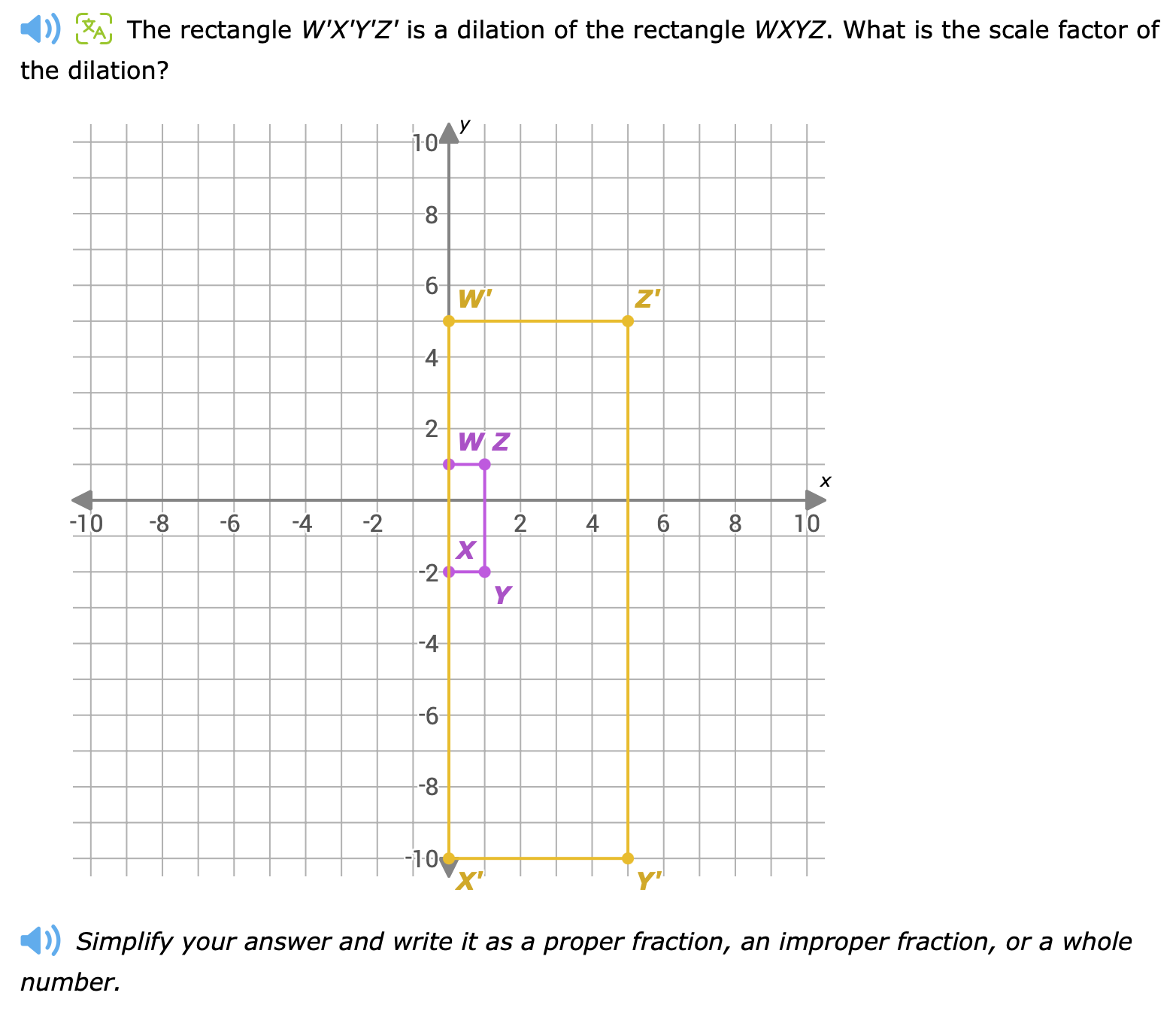
The rectangle W'X'Y'Z' is a dilation of the rectangle WXYZ. What is the scale factor of the dilation?

Steps to Solve

1. Identify the Coordinates of the Rectangles

First, we need to note the coordinates of points W, X, Y, Z for the original rectangle WXYZ and W', X', Y', Z' for the dilated rectangle W'X'Y'Z'.

From the graph:

• W(−2, 2), X(−2, −2), Y(2, −2), Z(2, 2)
• W'(−6, 6), X'(−6, −6), Y'(6, −6), Z'(6, 6)

2. Calculate the Lengths of the Sides for Each Rectangle

Next, we find the lengths of the sides of both rectangles.

For rectangle WXYZ:

• Length horizontally (W to Z) = 2 - (−2) = 4
• Length vertically (W to X) = 2 - (−2) = 4

For rectangle W'X'Y'Z':

• Length horizontally (W' to Z') = 6 - (−6) = 12
• Length vertically (W' to X') = 6 - (−6) = 12

3. Find the Scale Factor of the Dilation

The scale factor can be calculated using the formula:

$$ \text{Scale Factor} = \frac{\text{Length of Side in Dilated Rectangle}}{\text{Length of Side in Original Rectangle}} $$

Using side lengths for horizontal sides:

$$ \text{Scale Factor} = \frac{12}{4} = 3 $$

4. Verify with Vertical Dimensions

We can confirm the scale factor with the vertical dimensions:

$$ \text{Scale Factor} = \frac{12}{4} = 3 $$

Both calculations give the same scale factor.