The maximum value occurs when x =?
Understand the Problem
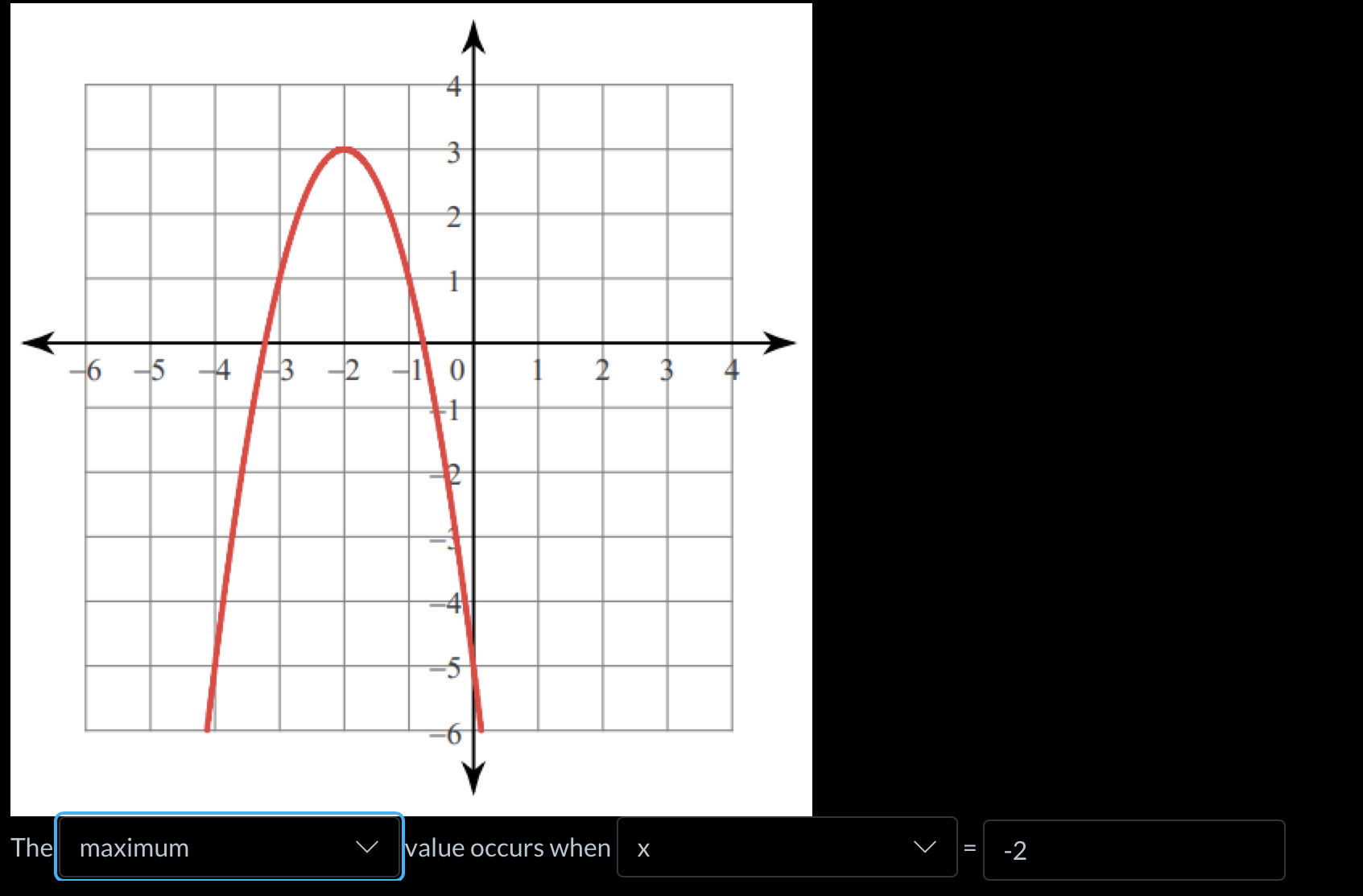
The problem is asking to identify at which x value the maximum of a parabola occurs. The graph of the parabola is provided, and it is clear that the maximum point (vertex) occurs at x = -2.
Answer
$-2$
Answer for screen readers
$-2$
Steps to Solve
- Identify the vertex
The vertex of the parabola is the highest point on the graph. Visually inspect the graph to find the coordinates of this point.
- Determine the x-coordinate
Read the x-coordinate of the vertex. This is the x-value where the maximum occurs.
- State the answer
The x-coordinate of the vertex is -2.
$-2$
More Information
The vertex of a parabola in the form $y = ax^2 + bx + c$ is given by the point $\left(-\frac{b}{2a}, f\left(-\frac{b}{2a}\right)\right)$. The x-coordinate of the vertex, $-\frac{b}{2a}$, tells us where the maximum or minimum value of the function occurs.
Tips
A common mistake is to confuse the x and y coordinates of the vertex. The problem asks for the x-value at which the maximum occurs, not the maximum value of the function (which would be the y-value).
AI-generated content may contain errors. Please verify critical information