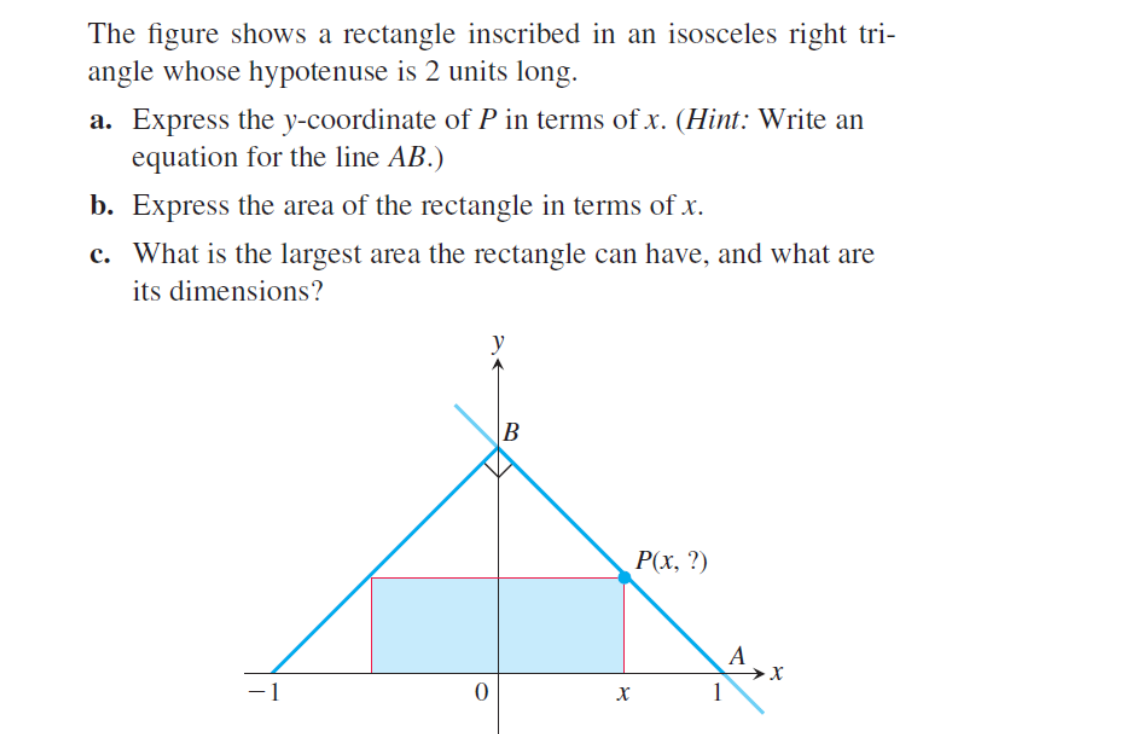
The figure shows a rectangle inscribed in an isosceles right triangle whose hypotenuse is 2 units long. a. Express the y-coordinate of P in terms of x. b. Express the area of the r... The figure shows a rectangle inscribed in an isosceles right triangle whose hypotenuse is 2 units long. a. Express the y-coordinate of P in terms of x. b. Express the area of the rectangle in terms of x. c. What is the largest area the rectangle can have, and what are its dimensions?
Understand the Problem
The question involves a rectangle inscribed in an isosceles right triangle. It asks for three tasks: to find the y-coordinate of a point in terms of x, to express the area of the rectangle in terms of x, and to determine the maximum area of the rectangle along with its dimensions.
Answer
The largest area the rectangle can have is 2 square units, with dimensions \(1\) unit in width and \(2\) units in height.
Answer for screen readers
The maximum area of the rectangle is 2 square units, with dimensions 1 unit (width) by 2 units (height).
Steps to Solve
- Find the equation of line AB.
The triangle is isosceles with vertices at A(1, 0), B(0, 2), and the origin O(0, 0). The slope of line AB (from A to B) can be calculated using the formula:
[ \text{slope} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 0}{0 - 1} = -2 ]
The equation of the line AB can be expressed in the slope-intercept form, (y = mx + b). To find (b), we can use point A(1, 0):
[ 0 = -2(1) + b \implies b = 2 ]
Thus, the equation of line AB is:
[ y = -2x + 2 ]
- Express the y-coordinate of P in terms of x.
Point P has coordinates ( (x, y) ). Using the line equation we found:
[ y = -2x + 2 ]
- Calculate the area of the rectangle.
The rectangle's width spans from (-1) to (x), so its width is:
[ \text{width} = x - (-1) = x + 1 ]
The height is simply the y-coordinate obtained above, (y = -2x + 2). Thus, the area (A) of the rectangle can be expressed as:
[ A = \text{width} \times \text{height} = (x + 1)(-2x + 2) ]
Expanding this gives:
[ A = -2x^2 + 2x - 2x + 2 = -2x^2 + 2 ]
- Maximize the area of the rectangle.
To find the maximum area, take the derivative (A' = -4x) and set it to zero:
[ -4x = 0 \implies x = 0 ]
Next, we evaluate the area at this critical point:
[ A(0) = -2(0)^2 + 2 = 2 ]
- Determine the dimensions of the rectangle.
At (x = 0), the width is:
[ \text{width} = x + 1 = 1 ]
And the height is:
[ y = -2(0) + 2 = 2 ]
Thus, the rectangle has dimensions (1 \times 2).
The maximum area of the rectangle is 2 square units, with dimensions 1 unit (width) by 2 units (height).
More Information
The rectangle's area depends on its width and height, derived from the relationship with the triangle's dimensions. The maximum area occurs at the vertex of the quadratic function representing the area.
Tips
- Failing to correctly compute the slope and equation of line AB.
- Not recognizing the area involves multiplying width and height.
- Ignoring the constraints on (x) when identifying maxima or minima.
