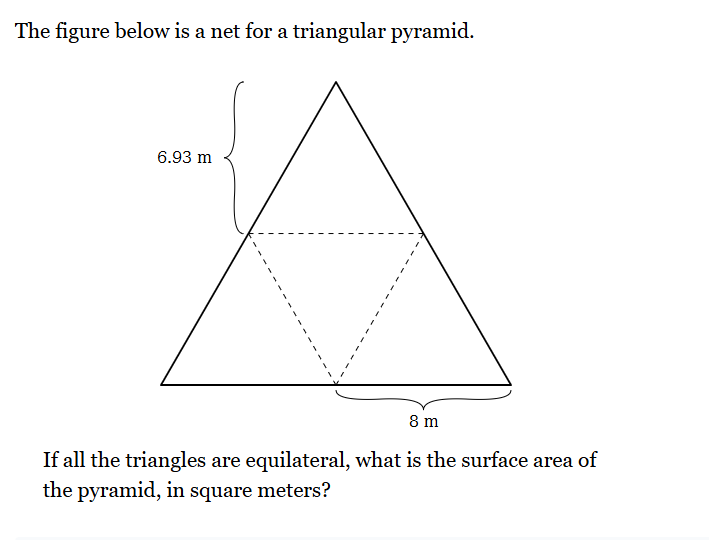
The figure below is a net for a triangular pyramid. If all the triangles are equilateral, what is the surface area of the pyramid, in square meters? The height of the triangle is... The figure below is a net for a triangular pyramid. If all the triangles are equilateral, what is the surface area of the pyramid, in square meters? The height of the triangle is 6.93 m and the base is 8 m.
Understand the Problem
The question provides a net of a triangular pyramid where all triangles are equilateral. The goal is to calculate the surface area of the pyramid in square meters, given the height and base of the triangles.
Answer
$110.88 \text{ m}^2$
Answer for screen readers
$110.88 \text{ m}^2$
Steps to Solve
- Calculate the area of one triangle
The area of a triangle is given by the formula $A = \frac{1}{2} \times base \times height$. In this case, the base is 8 m and the height is 6.93 m.
$$ A = \frac{1}{2} \times 8 \times 6.93 $$
$$ A = 4 \times 6.93 = 27.72 \text{ m}^2 $$
- Calculate the total surface area
Since the triangular pyramid is formed by 4 identical equilateral triangles, the total surface area is 4 times the area of one triangle.
$$ \text{Surface Area} = 4 \times 27.72 $$
$$ \text{Surface Area} = 110.88 \text{ m}^2 $$
$110.88 \text{ m}^2$
More Information
The surface area of the triangular pyramid is the sum of the areas of its four triangular faces. Since all the triangles are equilateral and identical, we only needed to calculate the area of one and multiply by four.
Tips
A common mistake is to only calculate the area of one triangle, forgetting that there are four triangles in the net. Another mistake would be using the wrong formula for the area of a triangle or incorrectly substituting the values for base and height.
AI-generated content may contain errors. Please verify critical information