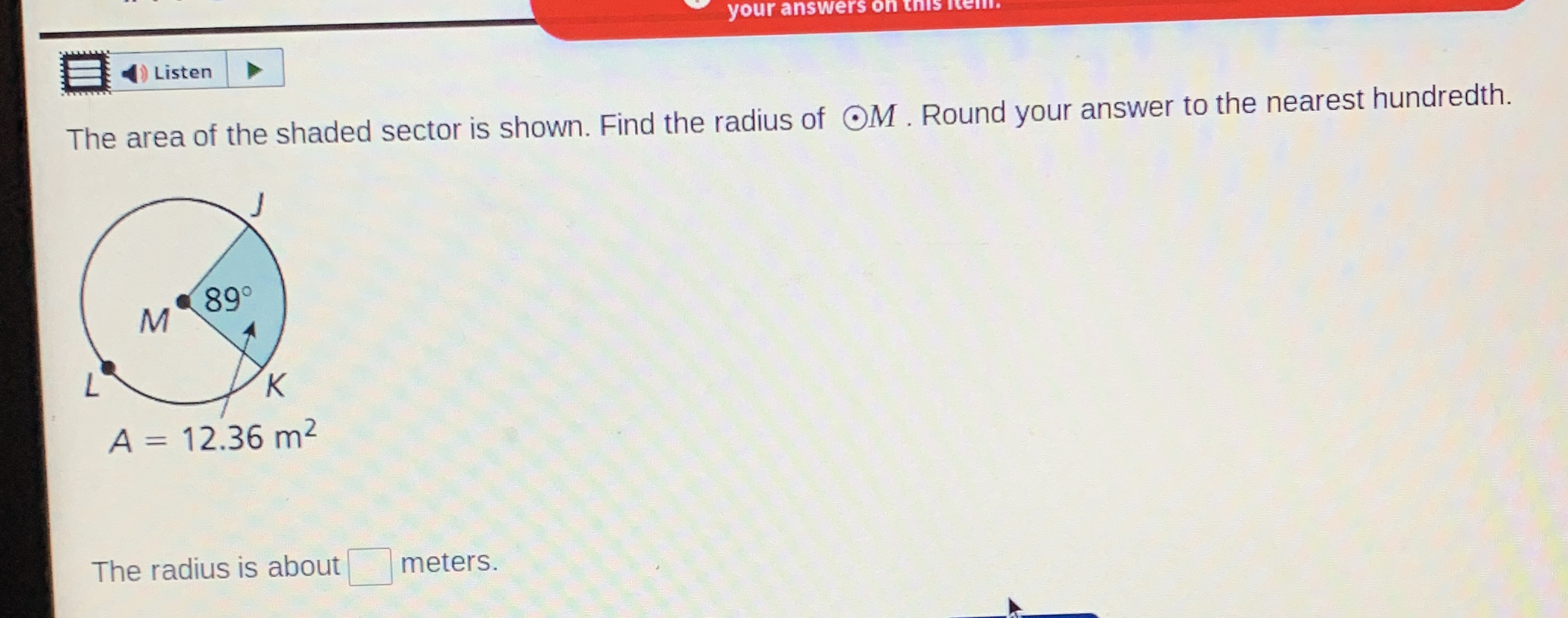
The area of the shaded sector is shown. Find the radius of the sector. Round your answer to the nearest hundredth.

Steps to Solve

1. Identify the relevant formula for the area of a sector

The area ( A ) of a sector can be calculated using the formula: $$ A = \frac{\theta}{360} \times \pi r^2 $$ where ( \theta ) is the angle in degrees and ( r ) is the radius.

2. Plug in the known values

Here, the area ( A = 12.36 , m^2 ) and the angle ( \theta = 89^{\circ} ). Substitute these values into the formula: $$ 12.36 = \frac{89}{360} \times \pi r^2 $$

3. Solve for ( r^2 )

To isolate ( r^2 ), rearrange the equation: $$ r^2 = \frac{12.36 \times 360}{89 \times \pi} $$ Now, calculate the right side.

4. Calculate ( r^2 )

First, compute ( 12.36 \times 360 ): $$ 12.36 \times 360 = 4450.4 $$

Next, calculate ( 89 \times \pi ): $$ 89 \times \pi \approx 89 \times 3.14159 \approx 279.252 $$

Now plug these values into the formula for ( r^2 ): $$ r^2 = \frac{4450.4}{279.252} $$

5. Determine ( r )

Calculate ( r^2 ): $$ r^2 \approx 15.95 $$

Now, take the square root to find ( r ): $$ r = \sqrt{15.95} \approx 3.99 $$

6. Round to the nearest hundredth

The final step is to round the radius to the nearest hundredth: $$ r \approx 4.00 $$