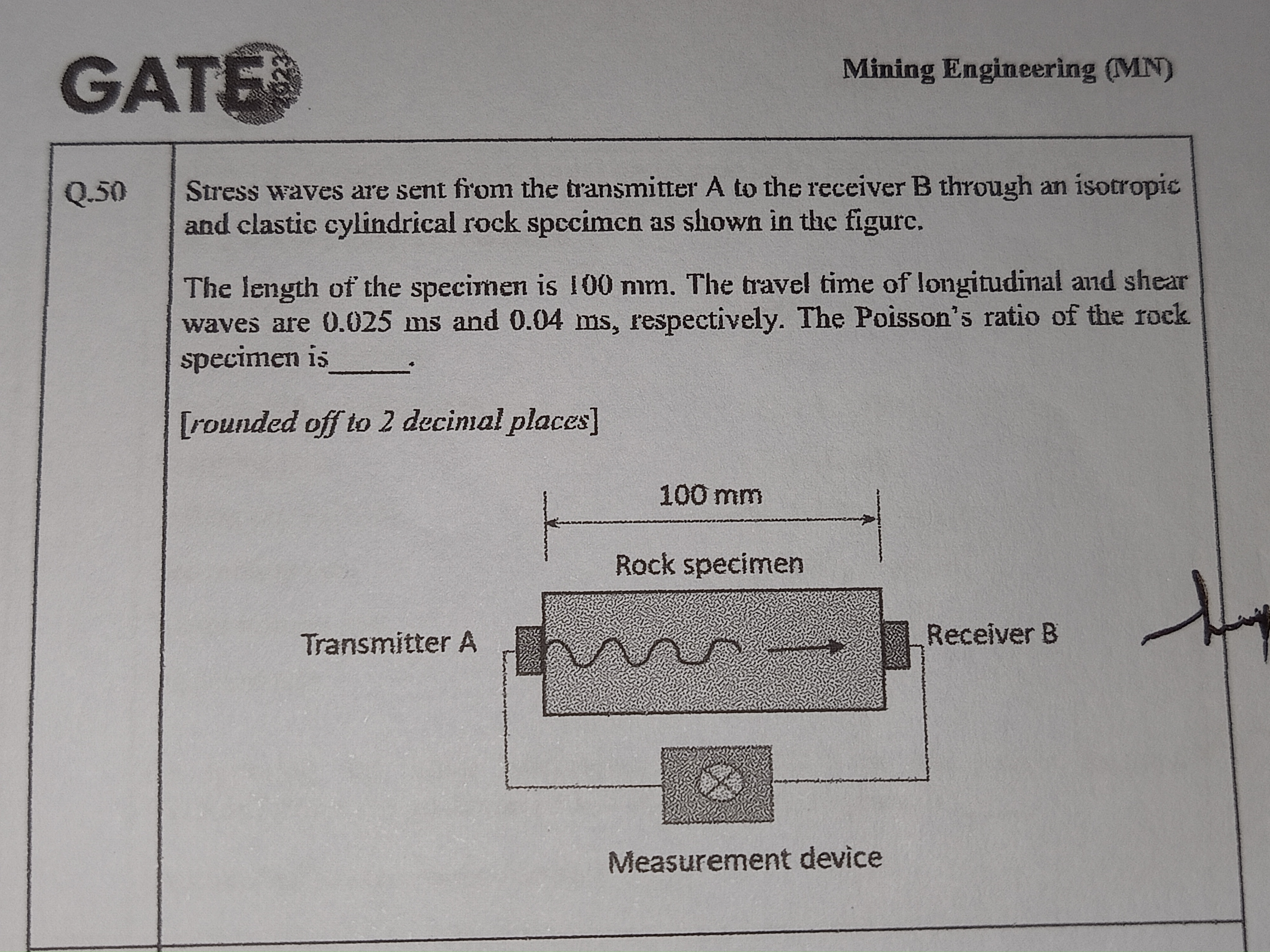
Stress waves are sent from the transmitter A to the receiver B through an isotropic and elastic cylindrical rock specimen. The length of the specimen is 100 mm. The travel time of... Stress waves are sent from the transmitter A to the receiver B through an isotropic and elastic cylindrical rock specimen. The length of the specimen is 100 mm. The travel time of longitudinal and shear waves are 0.025 ms and 0.04 ms, respectively. The Poisson's ratio of the rock specimen is _____ [rounded off to 2 decimal places]. Read more

Steps to Solve

1. Calculate wave speeds To find the speeds of the longitudinal and shear waves, we need to use the formula for wave speed, which is given by: $$ v = \frac{d}{t} $$ where $d$ is the distance and $t$ is the travel time.

For the longitudinal wave: $$ v_L = \frac{100 \text{ mm}}{0.025 \text{ ms}} = \frac{100 \times 10^{-3} \text{ m}}{0.025 \times 10^{-3} \text{ s}} $$

For the shear wave: $$ v_S = \frac{100 \text{ mm}}{0.04 \text{ ms}} = \frac{100 \times 10^{-3} \text{ m}}{0.04 \times 10^{-3} \text{ s}} $$

2. Calculate wave speeds numerically Calculating the speeds numerically, we have:

For longitudinal wave: $$ v_L = \frac{0.1 \text{ m}}{0.000025 \text{ s}} = 4000 \text{ m/s} $$

For shear wave: $$ v_S = \frac{0.1 \text{ m}}{0.00004 \text{ s}} = 2500 \text{ m/s} $$

3. Use the relation for Poisson's ratio For isotropic materials, Poisson's ratio $(\nu)$ can be calculated using the relation: $$ \nu = \frac{v_L^2 - 2v_S^2}{2(v_L^2 - v_S^2)} $$

Substituting the values obtained:

• $v_L = 4000 \text{ m/s}$
• $v_S = 2500 \text{ m/s}$

4. Calculate Poisson's ratio Let's compute the numerator and denominator:

Numerator: $$ v_L^2 - 2v_S^2 = 4000^2 - 2 \times 2500^2 $$

Denominator: $$ 2(v_L^2 - v_S^2) = 2(4000^2 - 2500^2) $$

Then calculate: $$ \nu = \frac{4000^2 - 2(2500^2)}{2(4000^2 - 2500^2)} $$

5. Final computation Calculate the individual components:

• $4000^2 = 16000000$
• $2500^2 = 6250000$

Now substitute: Numerator: $$ 16000000 - 2(6250000) = 16000000 - 12500000 = 3500000 $$

Denominator: $$ 2(16000000 - 6250000) = 2(9750000) = 19500000 $$

Then: $$ \nu \approx \frac{3500000}{19500000} $$

Calculate $\nu$ and round to two decimal places.