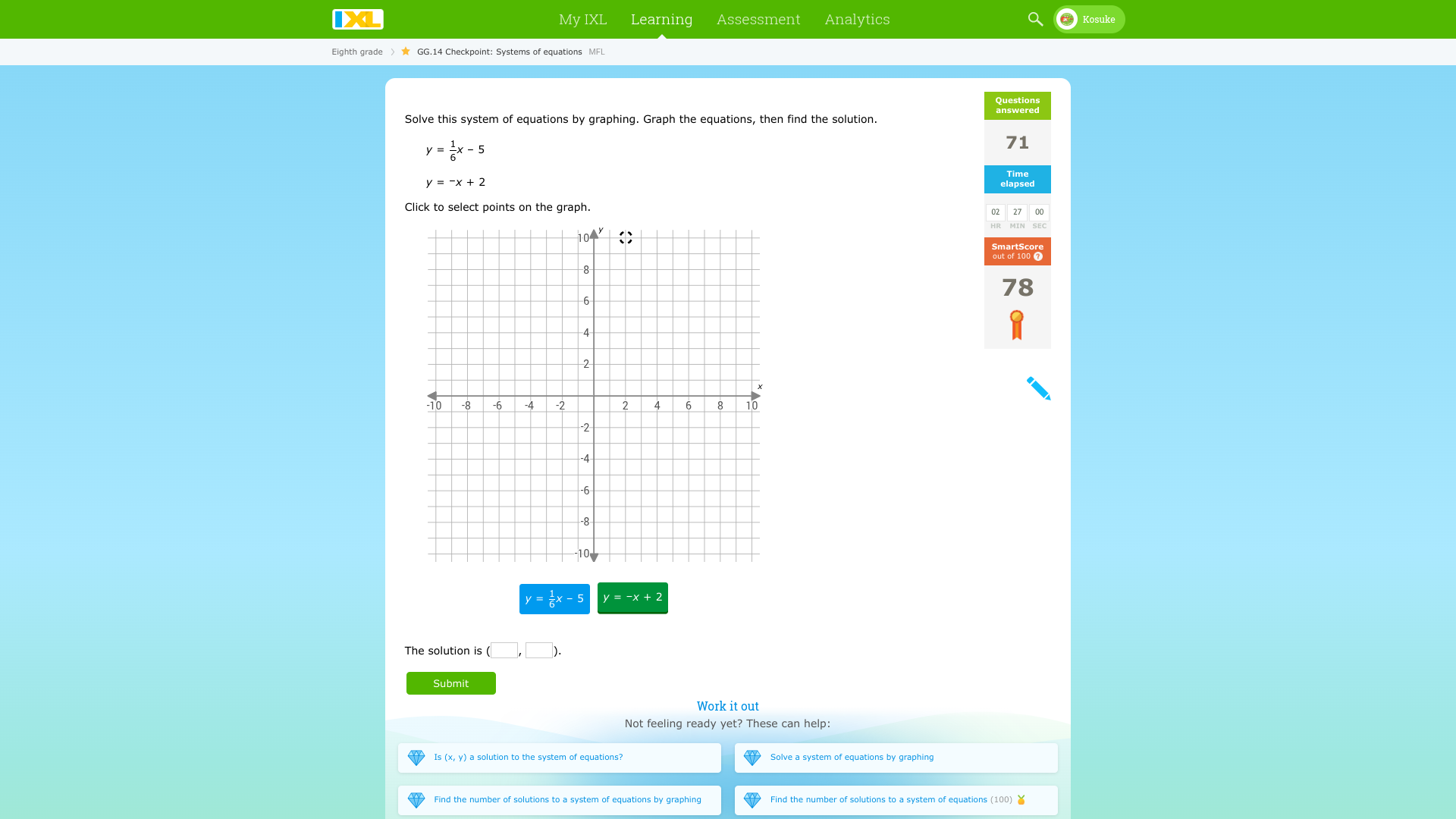
Solve this system of equations by graphing: y = 1/6x - 5 and y = -x + 2. Find the solution.

Understand the Problem

The question is asking to solve a system of equations by graphing. It provides two equations and requests the user to graph them and determine their intersection point, which represents the solution to the system.

Answer

The solution is $\left(-6, 0\right)$.

Steps to Solve

Write down the equations You have the equations:

$y = \frac{1}{6}x - 5$
$y = -x + 2$

Graph the first equation Start with the equation $y = \frac{1}{6}x - 5$.

The slope (m) is $\frac{1}{6}$ and the y-intercept (b) is $-5$.
Plot the y-intercept at (0, -5).
Use the slope to find another point: from (0, -5), go up 1 unit and right 6 units to (6, -4).
Draw a line through these points.

Graph the second equation Now graph the equation $y = -x + 2$.

The slope is -1 and the y-intercept is 2.
Plot the y-intercept at (0, 2).
From (0, 2), go down 1 unit and right 1 unit to (1, 1).
Draw a line through these points.

Find the intersection point Look for the point where the two lines cross. This point is the solution to the system of equations.
Identify the coordinates of the intersection Estimate the coordinates of the intersection point.

The solution is $\left(-6, 0\right)$.

More Information

The solution to the system of equations represents the values of $x$ and $y$ that satisfy both equations. In this case, $(-6, 0)$ means when $x = -6$, $y = 0$ satisfies both equations.

Tips

One common mistake is miscalculating a point when graphing the equations or misidentifying the intersection point. To avoid this, double-check the slope and y-intercept calculations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!