Solve the system of equations: 3*2^x - 4*7^y = -172 and 7*2^x + 2*7^y = 154.
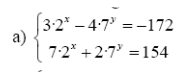
Understand the Problem
The question presents a system of equations involving exponential terms with variables x and y. It asks for a solution to this system of equations.
Answer
The solution is \( x = 3 \) and \( y = 2 \).
Answer for screen readers
The solution to the given system of equations is ( x = 3 ) and ( y = 2 ).
Steps to Solve
- Label the Equations
Let's label the two equations for easier reference:
- Equation (1): ( 3 \cdot 2^x - 4 \cdot 7^y = -172 )
- Equation (2): ( 7 \cdot 2^x + 2 \cdot 7^y = 154 )
- Rearranging Equation (1)
From Equation (1), isolate one of the variables. We can express ( 4 \cdot 7^y ) in terms of ( 2^x ): [ 4 \cdot 7^y = 3 \cdot 2^x + 172 ] Thus, [ 7^y = \frac{3 \cdot 2^x + 172}{4} ]
- Substituting in Equation (2)
Now, substitute the expression for ( 7^y ) into Equation (2): [ 7 \cdot 2^x + 2 \cdot \frac{3 \cdot 2^x + 172}{4} = 154 ]
- Simplifying the Equation
Multiply through by 4 to eliminate the fraction: [ 28 \cdot 2^x + 2(3 \cdot 2^x + 172) = 616 ] This simplifies to: [ 28 \cdot 2^x + 6 \cdot 2^x + 344 = 616 ]
- Combining Like Terms
Now combine the ( 2^x ) terms: [ 34 \cdot 2^x + 344 = 616 ]
- Isolate ( 2^x )
Subtract 344 from both sides: [ 34 \cdot 2^x = 272 ] Now divide by 34: [ 2^x = 8 ] Taking the logarithm or recognizing powers of 2 gives: [ x = 3 ]
- Finding ( y )
Substitute ( x = 3 ) back into the expression for ( 7^y ): [ 7^y = \frac{3 \cdot 2^3 + 172}{4} = \frac{24 + 172}{4} = \frac{196}{4} = 49 ] Taking roots, we find: [ 7^y = 7^2 \implies y = 2 ]
The solution to the given system of equations is ( x = 3 ) and ( y = 2 ).
More Information
This solution illustrates the use of substitution and algebraic manipulation to solve a system of exponential equations. The values found correspond to powers of 2 and 7, simplifying the calculations.
Tips
- Not properly simplifying expressions when substituting values.
- Forgetting to handle coefficients correctly during combination of terms.
- Confusing the bases when raising numbers to powers.
AI-generated content may contain errors. Please verify critical information