Solve the math problems presented in the image.

Understand the Problem

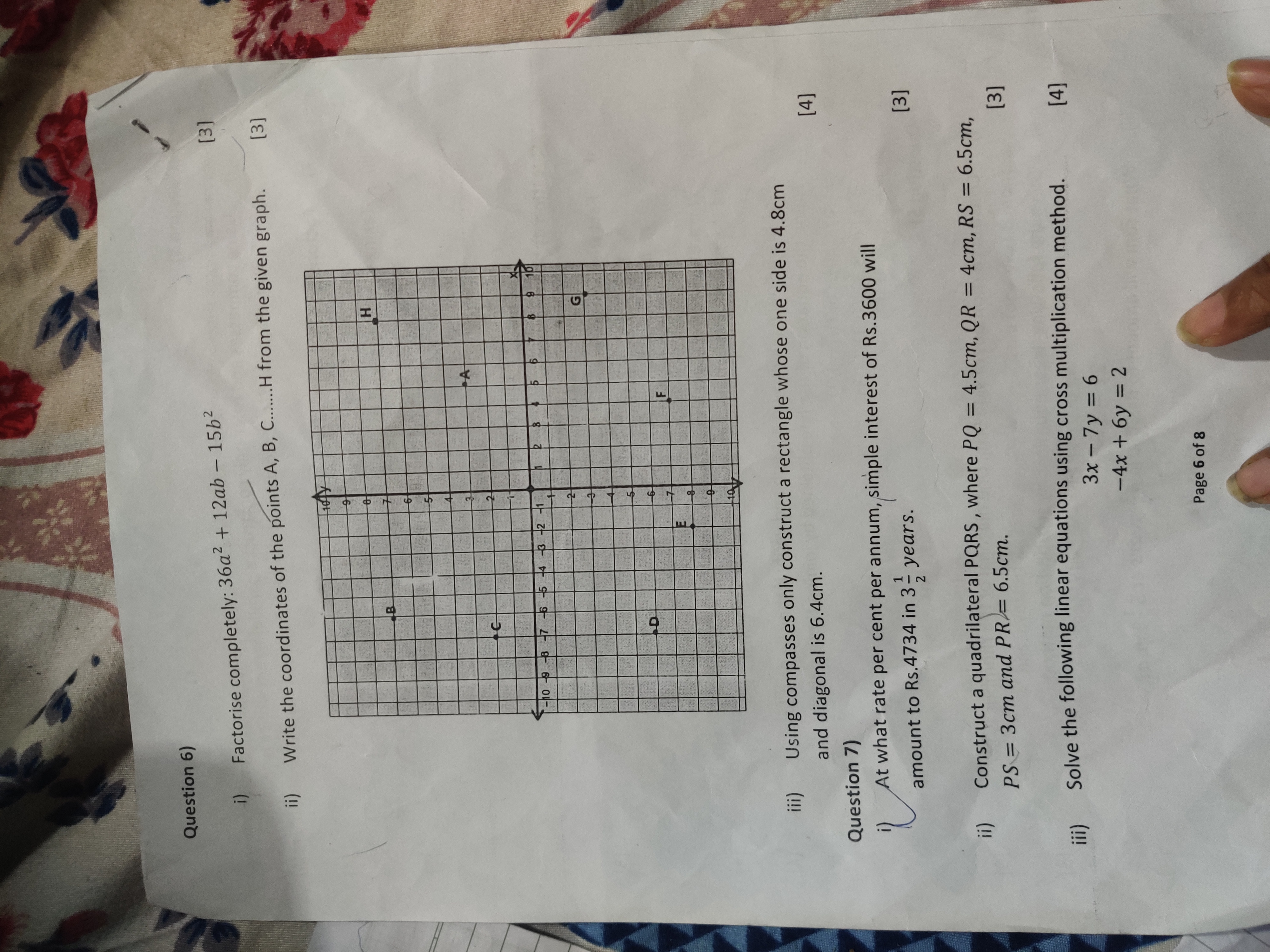
The image contains several math problems. The first problem asks to factorize a quadratic expression. The second problem asks us to determine the coordinates of the points A, B, C... H from the given graph. The third problem asks to construct a rectangle with one side being 4.8cm and the diagnonal being 6.4cm using compasses. The fourth problem asks to determine the rate per cent per annum, when the simple interest of Rs.3600 will amount to Rs.4734 in 3 1/2 years. The fifth problem asks to construct a quadrilateral PQRS, where PQ = 4.5cm, QR = 4cm, RS = 6.5cm, PS = 3cm and PR = 6.5cm. The last problem asks us to solve a system of linear equations in two variables using cross multiplication.

Answer

Question 6) i) $3(6a + 5b)(2a - b)$ ii) A(2, 4), B(-6, 6), C(-5, -7), D(-4, -5), E(0, -7), F(3, -4), G(6, 9), H(7, 8) Question 7) i) $9\%$ iii) $x = -5, y = -3$

Steps to Solve

Factorize $36a^2 + 12ab - 15b^2$

First, find the greatest common factor (GCF) of the coefficients 36, 12, and -15. The GCF is 3. Factor out the GCF from the expression:

$3(12a^2 + 4ab - 5b^2)$

Now, factor the quadratic expression $12a^2 + 4ab - 5b^2$. We are looking for two binomials of the form $(pa + qb)(ra + sb)$ such that $pr = 12$, $ps + qr = 4$, and $qs = -5$. By trial and error or using other factoring techniques, we find that:

$12a^2 + 4ab - 5b^2 = (6a + 5b)(2a - b)$

So, the completely factored expression is, $3(6a + 5b)(2a - b)$

Write the coordinates of the points A, B, C ... H from the given graph

Read the x and y coordinates directly off the graph for each shown point.

A = (2, 4) B = (-6, 6) C = (-5, -7) D = (-4, -5) E = (0, -7) F = (3, -4) G = (6, 9) H = (7, 8)

Determine the rate per cent per annum

The simple interest formula is $SI = \frac{PRT}{100}$, where SI is the simple interest, P is the principal, R is the rate per annum, and T is the time in years.

First determine the simple interest earned: $SI = 4734 - 3600 = 1134$

The Principal (P) = 3600 The Time (T) = $3\frac{1}{2}$ = 3.5 years

Substituting the above values into the formula. $1134 = \frac{3600 \times R \times 3.5}{100}$ $1134 = 36 \times R \times 3.5$ $1134 = 126R$ $R = \frac{1134}{126} = 9$

Therefore, the rate is 9% per annum.

Solve the linear equations using cross multiplication method

The given equations are: $3x - 7y = 6$ $-4x + 6y = 2$

Using cross multiplication method, we have: $\frac{x}{b_1c_2 - b_2c_1} = \frac{y}{c_1a_2 - c_2a_1} = \frac{1}{a_1b_2 - a_2b_1}$

Here, $a_1 = 3, b_1 = -7, c_1 = -6$ and $a_2 = -4, b_2 = 6, c_2 = -2$

Substituting these values, we get:

$\frac{x}{(-7)(-2) - (6)(-6)} = \frac{y}{(-6)(-4) - (-2)(3)} = \frac{1}{(3)(6) - (-4)(-7)}$ $\frac{x}{14 + 36} = \frac{y}{24 + 6} = \frac{1}{18 - 28}$ $\frac{x}{50} = \frac{y}{30} = \frac{1}{-10}$

Now, we can solve for x and y: $x = \frac{50}{-10} = -5$ $y = \frac{30}{-10} = -3$

Therefore, $x = -5$ and $y = -3$

Question 6) i) $3(6a + 5b)(2a - b)$ ii) A(2, 4), B(-6, 6), C(-5, -7), D(-4, -5), E(0, -7), F(3, -4), G(6, 9), H(7, 8)

Question 7) i) $9%$ iii) $x = -5, y = -3$

More Information

The cross-multiplication method is a simplified way to solve a system of two linear equations. The construction problems require geometric instruments like a compass and ruler, which are not solvable in text.

Tips

Forgetting to factor out the greatest common factor in factorization problems.
Making sign errors while using the cross-multiplication method.
Incorrectly reading the coordinates off the graph.
Errors in simple interest calculations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!