Evaluate each limit, if it exists, using any appropriate technique: a. lim (x->4) (16-x^2)/(x^3+64) b. lim (x->4) (x^2-16)/(x^2-5x+6) c. lim (x->-1) (x^2+x)/(x+1) d. lim (x->0) (sq... Evaluate each limit, if it exists, using any appropriate technique: a. lim (x->4) (16-x^2)/(x^3+64) b. lim (x->4) (x^2-16)/(x^2-5x+6) c. lim (x->-1) (x^2+x)/(x+1) d. lim (x->0) (sqrt(x+1)-1)/x e. lim (h->0) ((x+h)^2-x^2)/h f. lim (x->1) [(1/(x-1)) * (1/(x+3) - 2/(3x+5))] By using one-sided limits, determine whether each limit exists. Illustrate your results geometrically by sketching the graph of the function: a. lim (x->5) |x-5|/(x-5) b. lim (x->5/2) |2x-5|(x+1)/(2x-5) c. lim (x->2) (x^2-x-2)/|x-2| d. lim (x->-2) (x+2)^3/|x+2|
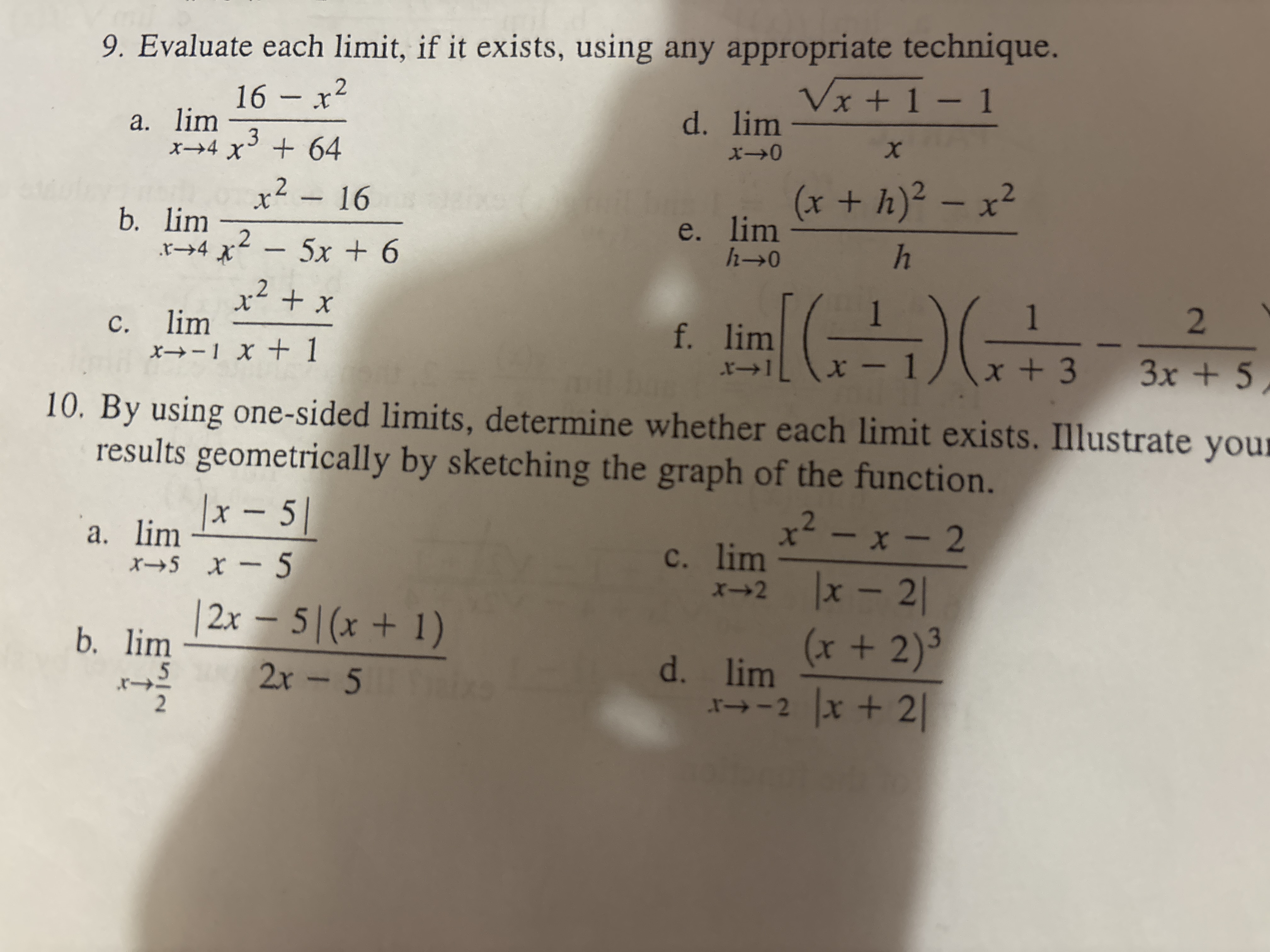
Understand the Problem
The question is asking to evaluate several limits using appropriate techniques, and determining if each limit exists by using one-sided limits and sketching the graph of the function. This requires knowledge of calculus, specifically limits, and the ability to apply various techniques to evaluate them.
Answer
9. a. 0 b. 0 c. -1 d. $\frac{1}{2}$ e. $2x$ f. $\frac{1}{32}$ 10. a. Does not exist b. Does not exist c. Does not exist d. 0
Answer for screen readers
a. $\lim_{x\to 4} \frac{16-x^2}{x^3 + 64} = 0$ b. $\lim_{x\to 4} \frac{x^2-16}{x^2 - 5x + 6} = 0$ c. $\lim_{x\to -1} \frac{x^2+x}{x+1} = -1$ d. $\lim_{x\to 0} \frac{\sqrt{x+1}-1}{x} = \frac{1}{2}$ e. $\lim_{h\to 0} \frac{(x+h)^2 - x^2}{h} = 2x$ f. $\lim_{x\to 1} [(\frac{1}{x-1}) * (\frac{1}{x+3} - \frac{2}{3x+5})] = \frac{1}{32}$ 10. a. $\lim_{x\to 5} \frac{|x-5|}{x-5}$ Does not exist b. $\lim_{x\to \frac{5}{2}} \frac{|2x-5|(x+1)}{2x-5}$ Does not exist c. $\lim_{x\to 2} \frac{x^2-x-2}{|x-2|}$ Does not exist d. $\lim_{x\to -2} \frac{(x+2)^3}{|x+2|} = 0$
Steps to Solve
- Evaluate $\lim_{x\to 4} \frac{16-x^2}{x^3 + 64}$
First, factor the numerator and denominator: $16 - x^2 = (4-x)(4+x) = -(x-4)(x+4)$ $x^3 + 64 = x^3 + 4^3 = (x+4)(x^2 - 4x + 16)$ So, $\frac{16-x^2}{x^3 + 64} = \frac{-(x-4)(x+4)}{(x+4)(x^2 - 4x + 16)} = \frac{-(x-4)}{x^2 - 4x + 16}$ for $x \ne -4$. Now, take the limit: $\lim_{x\to 4} \frac{-(x-4)}{x^2 - 4x + 16} = \frac{-(4-4)}{4^2 - 4(4) + 16} = \frac{0}{16} = 0$
- Evaluate $\lim_{x\to 4} \frac{x^2-16}{x^2 - 5x + 6}$
Factor the numerator and denominator: $x^2 - 16 = (x-4)(x+4)$ $x^2 - 5x + 6 = (x-2)(x-3)$ $\frac{x^2-16}{x^2 - 5x + 6} = \frac{(x-4)(x+4)}{(x-2)(x-3)}$ Take the limit: $\lim_{x\to 4} \frac{(x-4)(x+4)}{(x-2)(x-3)} = \frac{(4-4)(4+4)}{(4-2)(4-3)} = \frac{0}{2} = 0$
- Evaluate $\lim_{x\to -1} \frac{x^2+x}{x+1}$
Factor the numerator: $x^2 + x = x(x+1)$ $\frac{x^2+x}{x+1} = \frac{x(x+1)}{x+1} = x$ for $x \ne -1$ Take the limit: $\lim_{x\to -1} x = -1$
- Evaluate $\lim_{x\to 0} \frac{\sqrt{x+1}-1}{x}$
Multiply by the conjugate: $\frac{\sqrt{x+1}-1}{x} \cdot \frac{\sqrt{x+1}+1}{\sqrt{x+1}+1} = \frac{(x+1)-1}{x(\sqrt{x+1}+1)} = \frac{x}{x(\sqrt{x+1}+1)} = \frac{1}{\sqrt{x+1}+1}$ for $x \ne 0$ Take the limit: $\lim_{x\to 0} \frac{1}{\sqrt{x+1}+1} = \frac{1}{\sqrt{0+1}+1} = \frac{1}{1+1} = \frac{1}{2}$
- Evaluate $\lim_{h\to 0} \frac{(x+h)^2 - x^2}{h}$
Expand and simplify: $\frac{(x+h)^2 - x^2}{h} = \frac{x^2 + 2xh + h^2 - x^2}{h} = \frac{2xh + h^2}{h} = \frac{h(2x+h)}{h} = 2x + h$ for $h\ne0$ Take the limit: $\lim_{h\to 0} (2x + h) = 2x + 0 = 2x$
- Evaluate $\lim_{x\to 1} [(\frac{1}{x-1}) * (\frac{1}{x+3} - \frac{2}{3x+5})]$
Simplify the expression inside the limit: $\frac{1}{x+3} - \frac{2}{3x+5} = \frac{(3x+5)-2(x+3)}{(x+3)(3x+5)} = \frac{3x+5-2x-6}{(x+3)(3x+5)} = \frac{x-1}{(x+3)(3x+5)}$ Then, $\frac{1}{x-1} \cdot \frac{x-1}{(x+3)(3x+5)} = \frac{1}{(x+3)(3x+5)}$ for $x \ne 1$ Take the limit: $\lim_{x\to 1} \frac{1}{(x+3)(3x+5)} = \frac{1}{(1+3)(3(1)+5)} = \frac{1}{(4)(8)} = \frac{1}{32}$
- Evaluate $\lim_{x\to 5} \frac{|x-5|}{x-5}$
We need to consider the one-sided limits. For $x>5$, $|x-5| = x-5$, so $\frac{|x-5|}{x-5} = \frac{x-5}{x-5} = 1$. Thus, $\lim_{x\to 5^+} \frac{|x-5|}{x-5} = 1$. For $x<5$, $|x-5| = -(x-5)$, so $\frac{|x-5|}{x-5} = \frac{-(x-5)}{x-5} = -1$. Thus, $\lim_{x\to 5^-} \frac{|x-5|}{x-5} = -1$. Since the one-sided limits are not equal, the limit does not exist.
- Evaluate $\lim_{x\to \frac{5}{2}} \frac{|2x-5|(x+1)}{2x-5}$
We consider the one-sided limits. For $x>\frac{5}{2}$, $|2x-5| = 2x-5$, so $\frac{|2x-5|(x+1)}{2x-5} = \frac{(2x-5)(x+1)}{2x-5} = x+1$. Thus, $\lim_{x\to \frac{5}{2}^+} \frac{|2x-5|(x+1)}{2x-5} = \frac{5}{2} + 1 = \frac{7}{2}$. For $x<\frac{5}{2}$, $|2x-5| = -(2x-5)$, so $\frac{|2x-5|(x+1)}{2x-5} = \frac{-(2x-5)(x+1)}{2x-5} = -(x+1)$. Thus, $\lim_{x\to \frac{5}{2}^-} \frac{|2x-5|(x+1)}{2x-5} = -(\frac{5}{2} + 1) = -\frac{7}{2}$. Since the one-sided limits are not equal, the limit does not exist.
- Evaluate $\lim_{x\to 2} \frac{x^2-x-2}{|x-2|}$
We consider the one-sided limits. Factor the numerator $x^2 -x -2 = (x-2)(x+1)$ For $x>2$, $|x-2| = x-2$, so $\frac{(x-2)(x+1)}{x-2} = x+1$. Thus, $\lim_{x\to 2^+} x+1 = 3$. For $x<2$, $|x-2| = -(x-2)$, so $\frac{(x-2)(x+1)}{-(x-2)} = -(x+1)$. Thus, $\lim_{x\to 2^-} -(x+1) = -3$. Since the one-sided limits are not equal, the limit does not exist.
- Evaluate $\lim_{x\to -2} \frac{(x+2)^3}{|x+2|}$
We consider the one-sided limits. For $x>-2$, $|x+2| = x+2$, so $\frac{(x+2)^3}{x+2} = (x+2)^2$. Thus, $\lim_{x\to -2^+} (x+2)^2 = 0$. For $x<-2$, $|x+2| = -(x+2)$, so $\frac{(x+2)^3}{-(x+2)} = -(x+2)^2$. Thus, $\lim_{x\to -2^-} -(x+2)^2 = 0$. Since the one-sided limits are equal to $0$, the limit exists and is $0$.
a. $\lim_{x\to 4} \frac{16-x^2}{x^3 + 64} = 0$ b. $\lim_{x\to 4} \frac{x^2-16}{x^2 - 5x + 6} = 0$ c. $\lim_{x\to -1} \frac{x^2+x}{x+1} = -1$ d. $\lim_{x\to 0} \frac{\sqrt{x+1}-1}{x} = \frac{1}{2}$ e. $\lim_{h\to 0} \frac{(x+h)^2 - x^2}{h} = 2x$ f. $\lim_{x\to 1} [(\frac{1}{x-1}) * (\frac{1}{x+3} - \frac{2}{3x+5})] = \frac{1}{32}$ 10. a. $\lim_{x\to 5} \frac{|x-5|}{x-5}$ Does not exist b. $\lim_{x\to \frac{5}{2}} \frac{|2x-5|(x+1)}{2x-5}$ Does not exist c. $\lim_{x\to 2} \frac{x^2-x-2}{|x-2|}$ Does not exist d. $\lim_{x\to -2} \frac{(x+2)^3}{|x+2|} = 0$
More Information
- These limits were solved through factorization, simplification, rationalization and direct substitution.
- These limits were solved by considering the one-sided limits. If the one-sided limits agree, the limit exists and is equal to the one-sided limits. If the one-sided limits disagree, the limit does not exist.
Tips
- Forgetting to factor expressions completely, which can prevent simplification.
- Not considering one-sided limits when dealing with absolute values, which can lead to incorrect conclusions about the existence of a limit.
- Incorrectly applying algebraic manipulations, such as incorrectly multiplying by a conjugate or simplifying fractions.
AI-generated content may contain errors. Please verify critical information